SSPŠ APS Skripta
Vítejte ve skriptech předmětu APS na SSPŠ.
Tyto skripta slouží jako doplňující materiál k prezentacím a výkladu.
Veškeré organizační informace a materiály k předmětu najdete na předmětovém Moodlu.
Odevzdávání domácích úloh a opravené testy najdete na předmětové Submitty.
Autoři
- Michal Javor (prvotní verze skript v rámci maturitního projektu, 2023-2024)
- Bc. Michal Vojáček (učitel předmětu, 2024-)
- Studenti předmětu s PR na Githubu
Hradla a operátory Booleovy algebry
Jistě víte, že počítače pracují pouze s jedničkami a nulami. S pomocí pouze těchto dvou hodnot a operací nad nimi jsou schopné řešit libovolně komplikované problémy. Abychom mohli studovat, jak to je možné, musíme si určitým způsobem tyto základní výpočty nad jedničkami a nulami zformalizovat. Později si ukážeme, jak pomocí těchto jednoduchých operací stavět komplikovanější operace, moduly a finálně procesor.
Booleova algebra
Matematickou abstrakci pro výpočty pouze nad hodnotami 0 a 1 popsal v 19. století George Boole, nazývá se Booleova algebra. Tuto algebru můžeme zjednodušeně chápat jako alternativu ke klasické algebře z hodin matematiky - čísla a operace budou mít odlišný význam, než jsme zvýklí. Ovšem, pokud budou tyto operace chytře zvolené, jako v Booleově algebře, zjistíme, že spousta pravidel z klasické matematiky stále bude fungovat.
Výrazy v Booleově algebře
Podobně jako v matematice, budeme se zde zabývat výrazy. V takovém výrazu najdeme operátory, proměnné a neznámé. Např.
Zde je proměnná, která je definovaná tímto výrazem. jsou neznámé - musíme se k nim chovat jako by mohly mít libovolnou hodnotu. jsou operátory, které bychom uměli provést, pokud bychom znali hodnoty .
Nuly a jedničky
Každý výraz, proměnná nebo neznámá může v Booleově algebře nabýt pouze dvou hodnot:
- neboli
falseneboli nepravda neboli např. 0 voltů - neboli
trueneboli pravda neboli např. 5 voltů
U výpočtů v Booleově algebře se budeme držet hodnot a , nicméně je důležité si uvědomit, že tyto hodnoty mají jistý vztah k výrokové logice, která zkoumá, zda-li je nějaký výrok pravdivý (rečeno v Booleově algebře: výraz se rovná ). Zároveň se v praxi pak jedničky a nuly musí nějakým způsobem reprezentovat, například úrovní napětí na nějakém vodiči.
Operátory Booleovy algebry a hradla
Pozadí k operátorům
"Operátor" je pro naše účely symbol, který značí ve výrazu, že by se měla provést nějaké matematická operace, která bude mít nějaký výsledek. Operátory delíme podle počtu jejich argumentů (chcete-li "vstupů"):
- Unární (jeden vstup). V matematice máme např. unární mínus nebo faktoriál:
a - Binární (dva vstupy). Většina operátorů v matematice - sčítání, násobení, ...:
- Ternární a další. V matematice takových moc není, ale např. v programovaní narazíte na ternary conditional operator (a ? b : c).
Operátory v Booleově algebře
Protože v Booleově algebře mohou hodnoty nabývat pouze a , je velmi jednoduché zadefinovat chování takového operátoru: Stačí vypsat všechny možnosti! Takže například násobení () si můžeme zadefinovat takto:
A to je vše! Žádná jiná varianta nemůže nikdy nastat. Když se nad tím zamyslíme, tak ostatní operátory se od násobení budou lišit pouze pravou stranou rovnic - levá strana pouze vyčítá všechny možné kombinace a .
Další binární operátory si můžeme vymyslet vybráním / pro každou ze 4 variant vstupů. Takže binárních operátorů v Booleově algebře je pouze a násobení je jedním z nich. Celkem si zadefinujeme 6 binárních operátorů a 1 unární, které budeme bežně používat.
Pravdivostní tabulka
Uvidíme, že "vypsat všechny možnosti" je docela užitečná věc, nejenom pro základní operátory. Zavademe si tedy pravdivostní tabulku, ve které systematicky všechny možnosti popíšeme:
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Levá část pravdivostní tabulky je nadepsaná vstupy a vyčítá všechny jejich kombinace v přehledném (vzestupném) pořadí. V pravé straně máme výstup, který můžeme označít buď výrazem nebo proměnnou, například .
Pravdivostní tabulka má různý počet řádků podle počtu kombinací a tedy podle počtu vstupů. Každá kombinace vstupů se musí vyskutnout přesně jednou! Takže pro vstupných proměnných bude mít pravdivostní tabulka řádků.
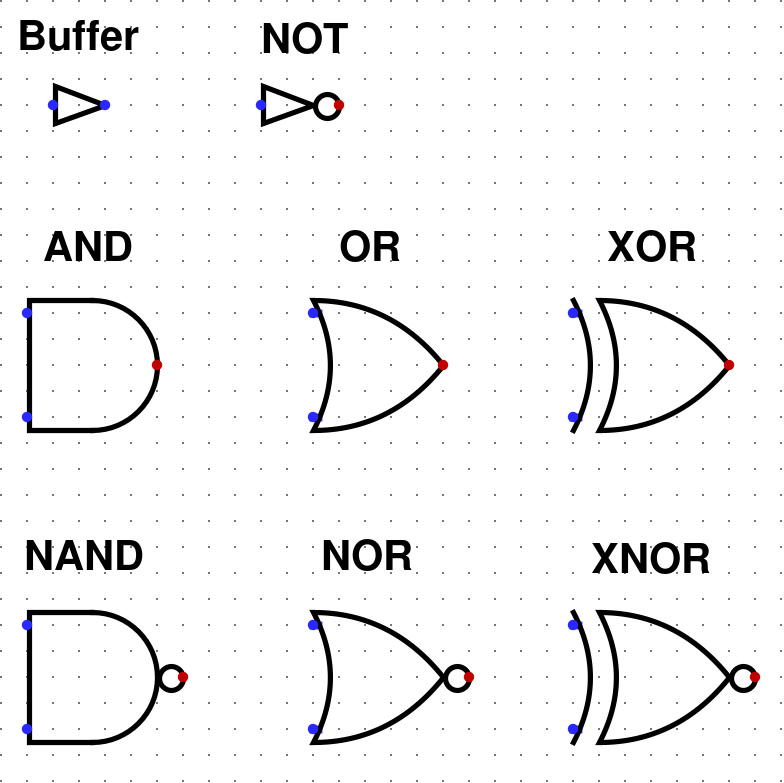
Hradlo
Ke každému, operátoru, který si ukážeme, si zavedeme hradlo. To je "fyzická krabička", která má Booleovské vstupy a výstupy, a umí "provést" danou operaci. Např. pro operaci násobení si zavademe hradlo AND:
Jde nám zde o tvar tohoto hradla, abychom ho uměli na první pohled rozlišit od ostatních. Stejně jako z operátorů lze stavět výrazy, z hradel budeme stavět obvody. Je důležité pamatovat na formální rozdíl mezi "operátorem" a "hradlem", ikdyž budeme používat "násobení" a "AND" zaměnitelně.
Výroková logika
K operátorům a značení, které si ukážeme, existuje ještě alternativní značení v tzv. výrokové logice, které se používá v matematice pro důkazy. Např. místo bychom napsali . Toto značení v tomto předmětu nepoužíváme, je uvedeno pro úplnost.
Unární operátory
Hradla, které mají jeden vstup jsou následující
- Buffer (repeater)
- NOT
Buffer (repeater)
Buffer je hradlo, u kterého výstup přesně kopíruje vstup. Nezavadíme pro něj symbol operátoru, protože je to zbytečné, trochu jako říkat v matematice místo . Nicméně v praxi se toto hradlo používá zejména pro zesílení signálu.
Symbol
Výraz
Matematická definice
Zápis v C
bool A;
bool Q = A;
Pravdivostní tabulka
| A | Q |
|---|---|
| 0 | 0 |
| 1 | 1 |
NOT
Hradlo NOT použijete, když potřebujete změnit hodnotu na její opak.
Neboli 0 → 1 nebo 1 → 0
Symbol
Definice
Matematická definice
Zápis v C
bool A;
bool Q = !A;
Pravdivostní tabulka
| A | Q |
|---|---|
| 0 | 1 |
| 1 | 0 |
Základní hradla se dvěma vstupy
Základní hradla, které mají dva vstupy jsou následující
- AND
- OR
- XOR
AND
Hradlo AND neboli logické "a" , se využívá když chcete naplnit dvě podmíky.
Pokud platí A a B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo AND rovná násobení
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A && B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR
Hradlo OR neboli logické "nebo" , se využívá když chcete naplnit aspoň jednu podmíku.
Pokud platí A nebo B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo OR rovná součtu
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A || B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR
Hradlo XOR neboli exkluzivní OR , se využívá když chcete naplnit pouze jednu podmíku. Jednoduše řečeno, když se sobě nerovnají.
*Pokud platí právě A nebo právě B, tak pošli na výstup hodnotu 1 ... Pokud se A nerovná B
Symbol
Definice
V Booleově algebře se pro hradlo XOR používá symbol
Zápis v C
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A ^ B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Opaky základních hradel se dvěma vstupy
Opaky základních hradel, existují právě 3
- NAND (opak AND)
- NOR (opak OR)
- XNOR (opak XOR)
NAND
Hradlo NAND má opačný výstup hradla AND
Pokud neplatí A a B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo NAND rovná negaci násobení
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A && B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR
Hradlo NOR má opačný vstup hradla OR
Pokud neplatí A nebo B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo NOR rovná negaci součtu
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A || B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR
Hradlo XNOR je opak hradla XOR, jednoduše řečeno se jedná o ekvivalenci
Pokud se A rovná B
Symbol
Definice
V Booleově algebře se hradlo XNOR rovná negaci operaci ((\oplus))
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A ^ B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Cheat sheet
Cheat sheet pro logické hradla
Vstup A a Vstup B dává výstup <operace>
| A | B | AND | OR | XOR | NAND | NOR | XNOR |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Zobrazení logických hradel v logisimu
Booleova algebra
Booleova algebra je algebraická struktura se dvěma binárními a jednou unární operací.
Jedná se o šestici (, , , , , ), kde je neprázdná množina
- Nejmenší prvek
- Největší prvek
- Unární operace (negace)
Budeme se soustředit na dvouprvkovou Booleovu algebru tj. budou 2 prvky:
- - ()
- - ()
Základní matematické symboly
| Název | Znak | Definice |
|---|---|---|
| Negace | nebo | Neguje vstup, tedy z 1 dostaneme 0 a obráceně |
| Disjunkce (spojení) | nebo | Logické nebo |
| Konjunkce (průsek) | nebo | Logické a |
Axiomy
| Název | Součet | Součin |
|---|---|---|
| komutativní | ||
| distrubutivní | ||
| neutralita 0 a 1 | ||
| agresivita 0 a 1 | ||
| vyloučení třetího |
Dualita Booleovy algebry
Prohozením a zároveň v celém obvodu/výrazu zůstane chování (logická funkce) zachovaná (samozřejmě při prohození 1 a 0 i na vstupech/výstupech). Toto chování vychází ze symetrie námi vybraných operátorů a k modelování Booleovy algebry.
| Výraz | Duální výraz |
|---|---|
De Morganovy zákony
| Zákon |
|---|
Zákon je efektivně lokální aplikací duality Booleovy algebry.
Pokud v nějaké sekci obvodu vyměníme (OR) za (AND) a obráceně, a na rozhraní sekce všechny znegujeme všechny signály (tím uvnitř sekce vyměníme 1 a 0), tak chování celého obvodu zůstane zachováno.
Z toho vyplývá, že lze vytvořit verzi De Morganových zákonů i pro 3 a více vstupů, klidně s odlišnými operátory.
Užitečné zákony
| Název | Součet | Součin |
|---|---|---|
| asociativní | ||
| o idempotenci prvků (absorbce) | ||
| absorbce | ||
| dvojí negace |
Hradlo XOR
Hradlo XOR můžeme kdykoliv zaměnit za disjunktivní normální formu (DNF) jeho logické funkce:
Karnaughova mapa
Karnaughova mapa je prostředek pro minimalizaci logických obvodů. Pro pochopení Karnaughovy mapy musíme první pochopit Grayův kód.
Grayův kód
Grayův kód je binární číselná soustava, ve které se každé dvě po sobě jdoucí hodnoty liší v jedné bitové pozici.
Příkladná tabulka pro 3 bity (tučně zvýrazněný změněný bit):
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
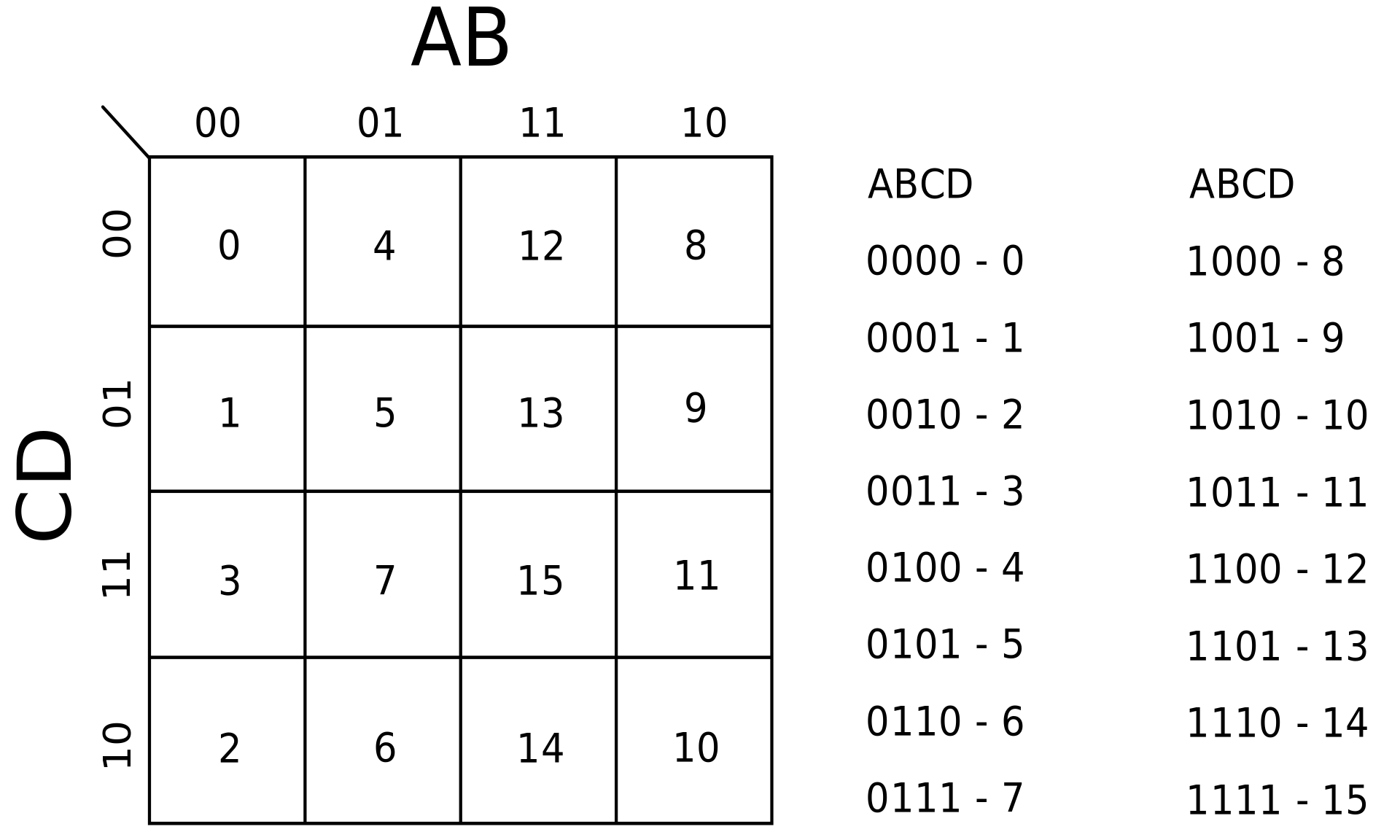
Karnaughova mapa - příklad 1
Máme pravdivostní tabulku se vstupy a výstupem :
| A | B | C | D | Q | index bitu |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 2 |
| 0 | 0 | 1 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 0 | 5 |
| 0 | 1 | 1 | 0 | 0 | 6 |
| 0 | 1 | 1 | 1 | 0 | 7 |
| 1 | 0 | 0 | 0 | 1 | 8 |
| 1 | 0 | 0 | 1 | 1 | 9 |
| 1 | 0 | 1 | 0 | 1 | 10 |
| 1 | 0 | 1 | 1 | 1 | 11 |
| 1 | 1 | 0 | 0 | 1 | 12 |
| 1 | 1 | 0 | 1 | 1 | 13 |
| 1 | 1 | 1 | 0 | 0 | 14 |
| 1 | 1 | 1 | 1 | 0 | 15 |
- Vytvoříme tabulku pomocí indexů v pravdivostní tabulce (odvíjí se od Grayova kódu). Neboli doplníme do obrázku
Vznikne nám následující tabulka
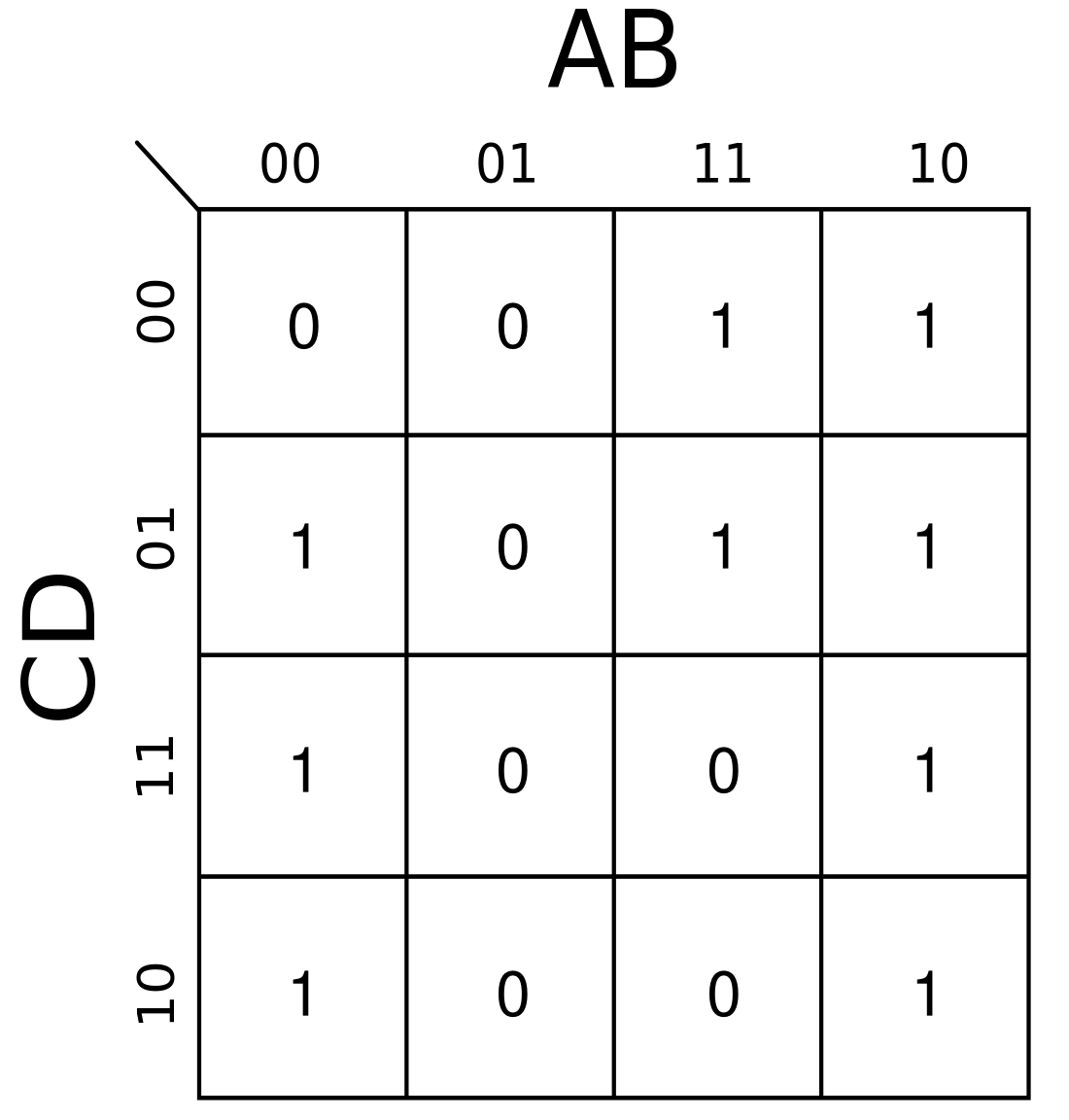
- Zakroužkujeme sousedy
Musíme zakroužkovat všechny , kroužkujeme buď samostatnou (v tomto případě je výsledek stejný jako při stavění pomocí mintermů přímo z pravdivostní tabulky, tady K-mapa nemá žádný přínos) nebo obdélníky s obsahem rovným některé mocnině , z čehož přímo vyplývá (jako nutná podmínka), že obě délky stran obdélníků musí být mocniny dvou.
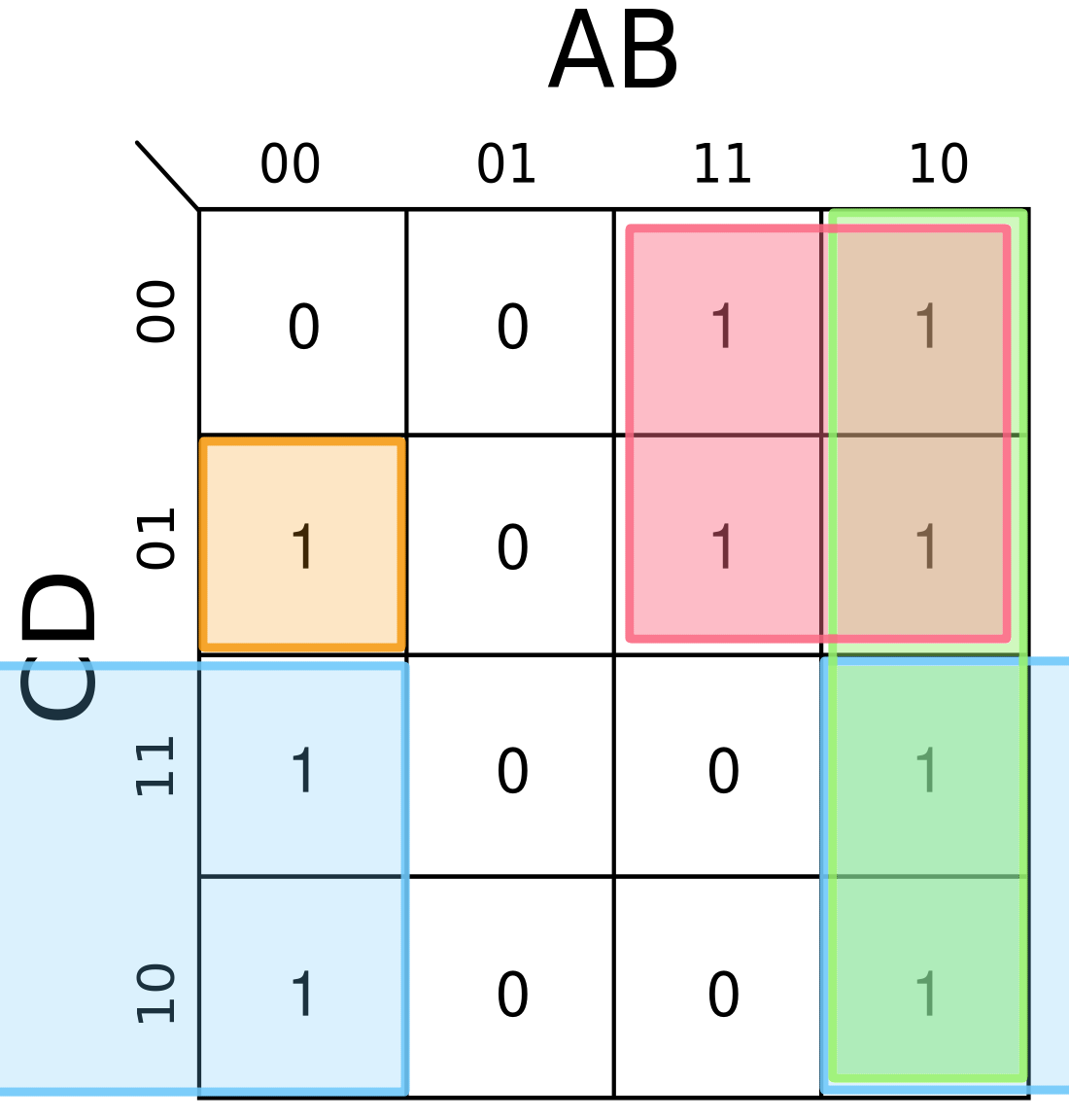
- Vytvoříme výrazy
- Růžová -
- Zelená -
- Modrá -
- Oranžová -
- Sečteme výrazy
- Upravíme výraz
Karnaughova mapa - příklad 2
Máme pravdivostní tabulku se vstupy a výstupem :
| A | B | C | Q |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
- Vytvoříme si Karnaughovu mapu (tam kde jsou písmena, tak je hodnota nastavená na 1)
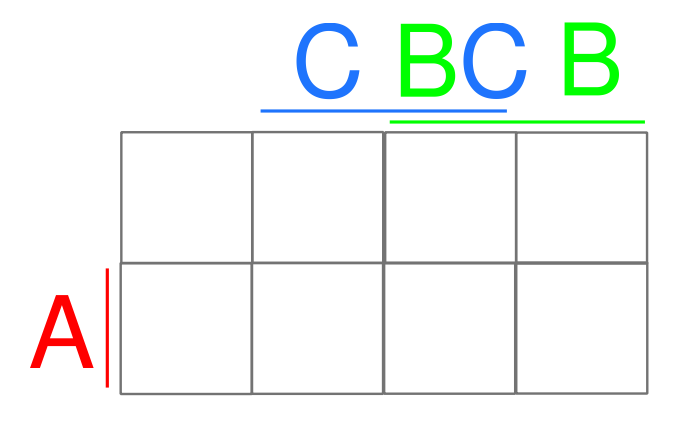
- Doplníme do tabulky

- Zakroužkujeme největší obdelníky a vyjádříme je
POZOR: oranžový 1x1 obdélník není optimální (maximální), lepší by byl jako 2x2 čtverec přecházející přes hranu. Je to takhle zvolen abychom ukázali, že K-Mapa dál funguje, jenom není výsledek optimální - 1x1 čtverec je potřeba vyjádřit jako 4-term, místo 2-termu pokud bychom udělali 2x2.

Vidíme, že je blok nezávislý na tom, jestli je nebo , takže zahrneme jen proměnné a
- musí být
- musí být
Součin jsme použili, protože je totožné logickému a zároveň platí (v programovacím jazyku C -->&&)
Jelikož se jedná o torus (viz. gif), můžeme označit i hodnoty, které se nacházejí "vedle sebe" (na začátku a na konci)

Vidíme, že je výraz nezávislý na proměnné (může být nebo )
- musí být
- musí být
- Sjednotíme výrazy
Výsledné výrazy sečteme
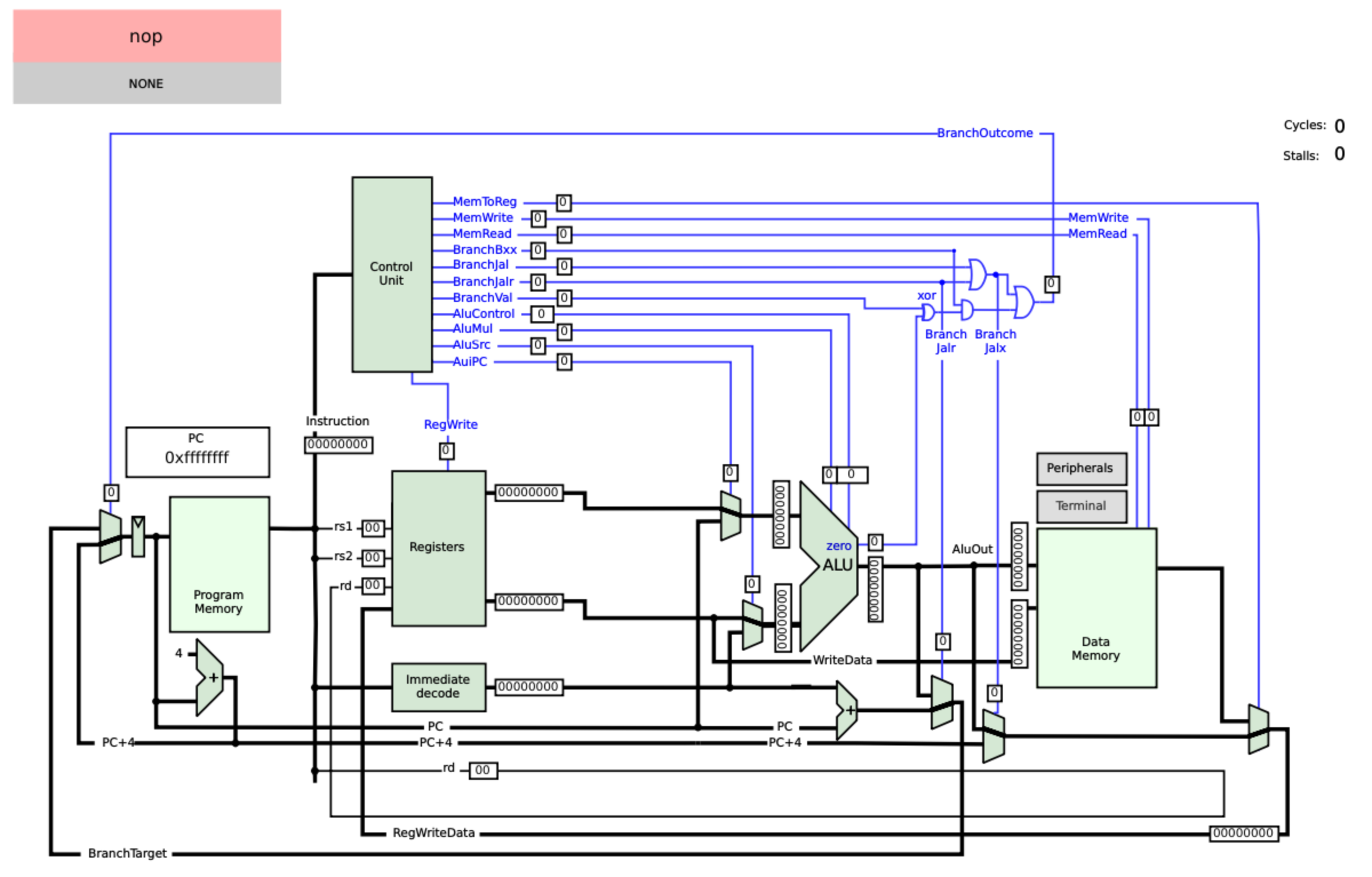
- Výsledný výraz si můžeme postavit v logisimu viz. obrázek
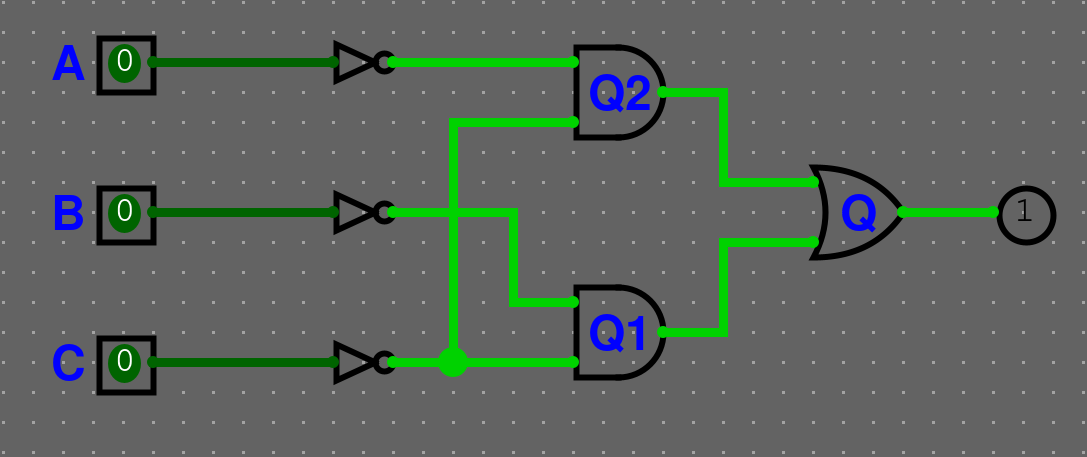
- Zkontrolujeme pravdivostní tabulku.
- Klikneme pravým tlačítkem na circuit v nabídce (základní je main)
- Klikneme na tlačítko Build Circuit
- Potvrdíme tlačítkem OK, popřípadě Yes
- Vybereme v nabídce Table
- Dostaneme tabulku viz. obrázek

Příprava na první test
Znalost hradel a operátorů Booleovy algebry
V tomto předmětu používáme hradla:
- BUFFER, NOT
- AND, NAND
- OR, NOR
- XOR, XNOR
Existují i další hradla (zejména implikace () ve výrokové logice), ale ty nebudeme potřebovat.
Ke každému hradlu je potřeba znát:
- Název (AND)
- "Distinctive shape" tvar hradla (podle IEEE Std 91/91a-1991)
- Výraz/operátor v Booleově algebře ()
- Pravdivostní tabulku, neboli jeho chování
V testu je potřeba na základě jednoho z těchto údajů vypsat všechny 3 ostatní, pro všechny hradla.
Podle názvu
Nakresli logická hradla, zapiš operátor hradla jako výraz (např. X=A+B), nakresli pravdivostní tabulku.
a) NOT
b) OR c) XNOR d) ANDPodle tvaru
a)
Podle výrazu nebo podle tabulky
I to se může stát.
Převod mezi obvodem, výrazem a pravdivostní tabulkou
V prvním testu stačí pouze:
- obvod tabulka
- výraz tabulka
- obvod výraz
Pokud k tomu nejste explicitně vyzváni, výraz žádným způsobem neupravujte/neminimalizujte! Správný výraz je ten, který přesně odpovídá zadanému zapojení (vyjma: komutativity, asociativity).
obvod výraz
1)

2)

výraz obvod a tabulka
Řešení - zapojení
Řešení - zapojení

Taktéž v zapojení lze použít jeden třívstupový OR, jelikož sčítání je asociativní a komutativní.
Řešení - tabulka
Řešení - tabulka
Vytváření tabulky si ulehčíme spočítáním sloupců pro námi zvolené podvýrazy (, a ). Jejich hodnoty použijeme v dalších výpočtech, abychom se vyhnuli chybám při počítání komplikovaných výrazu z hlavy. Pokud víme na první pohled hodnoty některých řádků výsledku, můžeme je vyplnit hned do výsledku a v pomocných sloupcích je přeskočit. Nutné sloupce jsou pouze vstupy (,,) a výstupy ().
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Je důležité aby tabulka byla dobře zarovnaná a aby její řádky byly seřazené podle numerické hodnoty vstupů, pro lepší čitelnost.
Cvičebnice
Pro další procvičování je zde k dispozici 8 dalších logických funkcí ve všech tří nám známých reprezentacích. Rozbalte si jednu z nich jako zadání a snažte se vytvořit ostatní dvě (pokud byl tento postup již probrán). Navíc je zde uvedený minimální výraz pro danou logickou funkci, který se bude hodit na procvičování zjednodušování výrazů.
X1
X2
X3
X4
X5
X6
X7
X8
Příprava na druhý test
5. Zjednoduš následující výraz do co nejjednodušší podoby
Výsledek zde:
Řešení
absorbce, De Morgan, absorbce
asociativita, vyloučení třetího a neutralita 0
idempotence, vyloučení třetího
agresivita 1
Výsledek zde:
Řešení
De Morgan, absorbce
distributivita (vytkutí násobení)
vyloučení třetího a neutralita 1
absorbce
Pro další procvičení mohou posloužit příklady ze cvičebnice pro první test, kde je uvedená i minimalizovaná podoba výrazu.
Instalace a nastavení Logisim Evolution
Pozor na to, že používate Logisim Evolution. Klasický Logisim je už léta zastaralý, je nestabilní, nepodporuje moderní komponenty, a projektové soubory s Logisimem Evolution nejsou kompatibilní!
Logisim template
Nastavte si v Logisimu template: File > Preferences... > Template > User template > Select > Vybrat template file
Šablona je nastavená tak, aby komponenty odpovídaly doporučenému vizuálnímu stylu (narrow gates).
Instalace logisimu
Windows (pozn: na školních PC je nutné provést manuální instalaci)
Linux: níže
Linux
Flatpak: flatpak install com.github.reds.LogisimEvolution
Snap: snap install logisim-evolution
Případně další metody zde, nebo manuální instalace níže.
Manuální instalace
Java 21
Logisim Evolution od verze 3.9.0 vyžaduje Javu 21.
Linux
Nejpřímočařejší nainstalovat openjdk z repozitářů, e.g. na ubuntu:
apt-get install openjdk-21-jre
Windows
Doporučuji Microsoft build openjdk, protože se hezky zaintegruje do windows a aplikace to můžou bez problému najít. Pro windows tedy instalátor .msi. Během instalace je vhodné vybrat všechny features, tedy i nastavení JAVA_HOME a Oracle registry keys.
Instalace bez administrátorských práv (e.g. ve škole)
Instalace bez administrátorských práv (e.g. ve škole)
V případě, že nemáte k dispozici administrátorské práva, postačí .zip openjdk, který si rozbalíte, a do jeho bin složky (vedle java.exe) nakopírujete logisim. Přes shift-rightlick můžete pak ve složce otevřít terminál, ve kterém lze logisim spustit přes
.\java.exe -jar logisim-evolution-xxxx.jar
Je důležité mít .\ před java.exe, jinak se použije systémová, potenciálně zastaralá, java.
Logisim Evolution
Obecně stáhneme z oficiálního git repa v releases https://github.com/logisim-evolution/logisim-evolution/releases nejnovější verzi.
Tedy
- Debian based (e.g. Ubuntu) -
.deb - RPM package -
.rpm - Windows -
.msi - macOS -
.dmg - Ostatní -
.jar- půjde spustit buď poklikáním nebo z terminálu pomocíjava -jar logisim-evolution-xxx.jar
Na linuxu pozor na instalaci z repozitářů distribuce (apt, dnf, yum, flatpak, snap, ...). Často v nich bývají zastarelé verze, které nemají pro nás potřebné bugfixy a features (třeba autosave)!
Arch linux
Můžeme nainstalovat z Arch AUR repozitáře pomocí yay
yay -S logisim-evolution-bin
Pokud preferujete instalaci ze zdrojáku, můžete vynechat -bin.
Logisim - Základy
Pozor na to, že používate Logisim Evolution. Klasický Logisim je už léta zastaralý, je nestabilní, nepodporuje moderní komponenty, a projektové soubory s Logisimem Evolution nejsou kompatibilní!
Po úspěšném nainstalovaní logisim-evolution (viz. návod) a spuštěním, uvidíte tohle:
Template
Jako první vám doporučuji nahrát template, kde jsou všechny gaty nastavené na narrow.
Nahrajeme template:
File --> Open --> vybereme template.circ soubor, který jsme stáhli.
Uložíme zvlášť, abychom nepřepsali náš template:
File --> Save As --> Uložíme nový soubor (taky můžeme použít zkratku Ctrl + Shift + S)
Základy
Kurzory
Kurzory se nachází v horním menu, levým kliknutím můžeme vybrat kurzor.

Jsou celkem 4
- Červený kurzor - interaktivní kurzor, měníme pomocí něj hodnoty nebo se pohybujeme v logickém obvodu
- Černý kurzor - měníme zapojení, vkládáme různé komponenty
- Dráty - tvoření drátů
- Text - na popsání obvodu
Kurozry můžeme měnit pomocí zkratky
Ctrl + [1-4]
První obvod
V zeleném obdélníku se vyskytují složky obsahující různé komponenty.
Zadání
Vytvořte logický obvod, který se bude chovat úplně stejně jako logický AND.
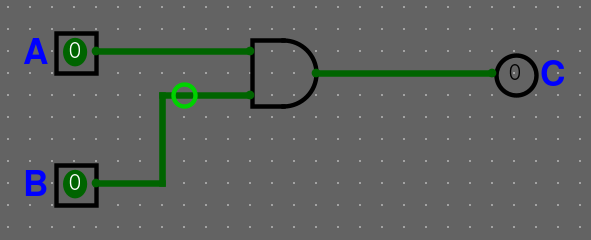
První si vytvoříme nový obvod a to tím, že klikneme pravým tlačítkem na název našeho projektu (složka ve ktéré máme obvod main). U mě je to logisim-uvod viz. obrázek
Klikneme na Add Circuit a zvolíme jméno obvodu třeba custom_and, potvrdíme a klikneme na něj dvakrát pro otevření.
První rozklikneme složku Wiring a klikneme na komponent Pin. Komponent přetáhneme do obvodu dvakrát (AND má 2 vstupy)

Poté tam dáme AND, který najdeme v Gates/AND Gate klikneme na komponentu a přidáme ji.
Taky musíme přidat výstup (output pin), což je vlastně Pin. Takže přetáhneme komponentu do obvodu.

Klikneme na náš pin a změníme jeho vlastnosti na následující.
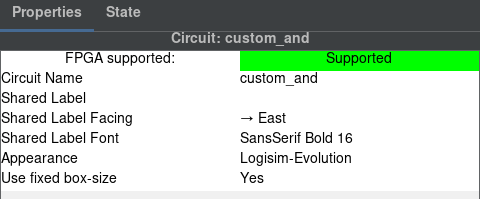
Nezbývá nám nic jiného než obvod propojit a máme následující logický obvod. Přidáme labely pro přehlednost, které taky najdeme ve vlastnostech.
Náš nově vytvořený obvod vložíme do main
- Klikneme dvakrát na
main - Vybereme
custom_anda vložíme do obvodu - Přidáme nějaké input a output piny pro testování
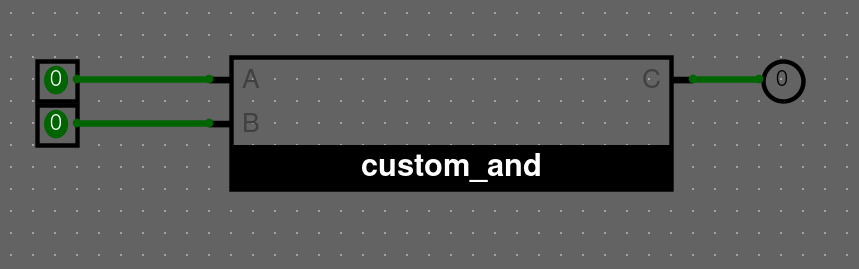
Následovně můžeme měnit hodnotu input pinů a to tak, že vybereme červenou ruku nahoře v nabídce nebo pomocí zkratky Ctrl + 1
Vlastnosti komponent
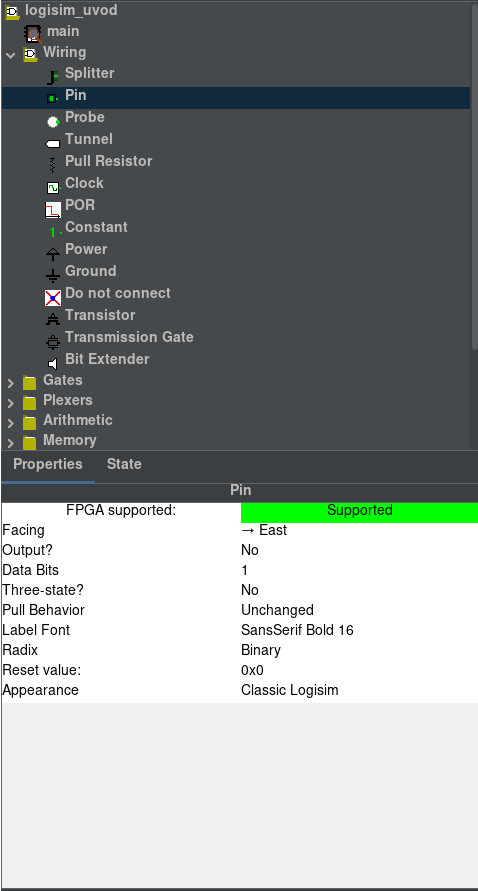
Jsou 2 možnosti jak změnit vlastnosti komponent:
- Pouze pro jednu instanci komponentu
- Změníme pomocí vybrání komponentu v obvodu
- Pro všechny instance kompenentu
- Změníme pomocí vybrání komponentu v nabídce
Nejčastěji upravované vlastnosti jsou:
Facing- Otočení komponentyLabel- Text u komponentyGate Size- Velikost hradlaOutput?- Jestli jePinoutput nebo ne
Cvičení
Vytvořte podobné obvody pro OR a XOR.
Třetí stav a zkraty
Váš obvod může mít 4 stavy
0- Vypnutý stav1- Zapnutý stavU- Třetí stav (undefined)E- Zkrat
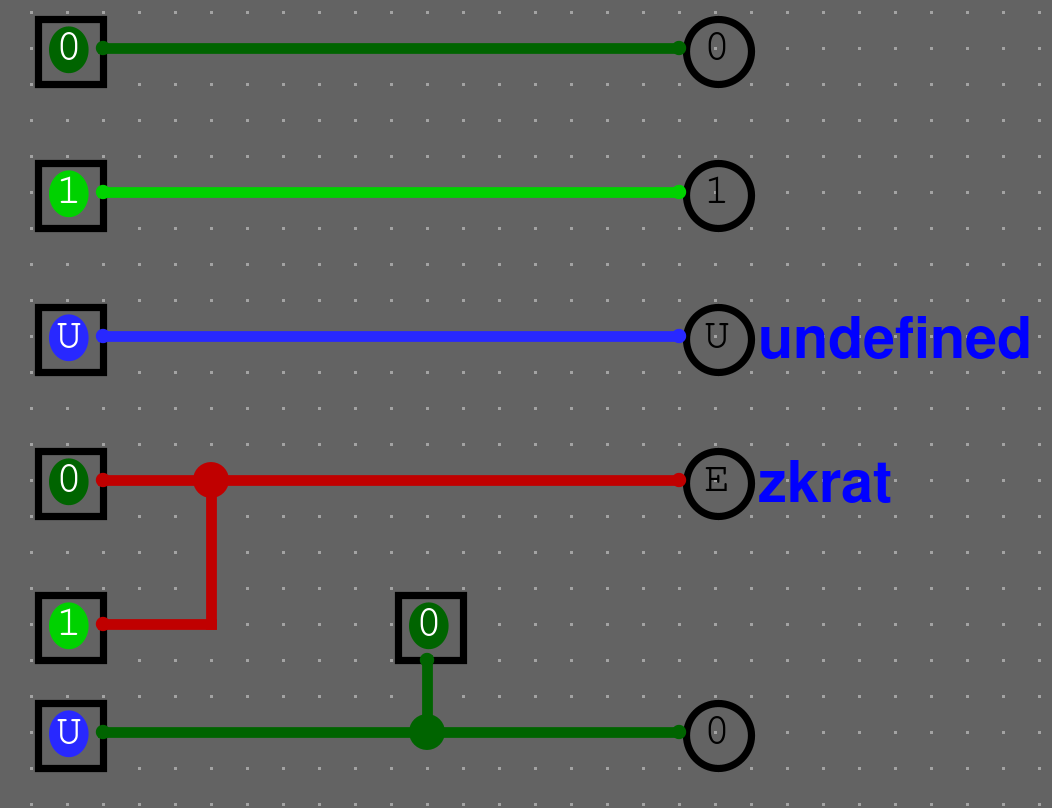
Legitimní stavy
0- Vypnutý stav1- Zapnutý stavU- Třetí stav (undefined)
Legitimní stavy jsou všechny kromě zkratu. Občas se tedy stane, že i třetí stav je žádoucí.
Třetí stav
Třetí stav je nedefinovaná hodnota. Příkladné použití je pomocí Controlled Buffer (Najdeme v Gates/Controlled Buffer). Tenhle komponent vám buď propustí proud, nebo ne.
Příklad
Máme následující obvod. Pokud nic nepouštíme, máme třetí stav, hodnota není definovaná.
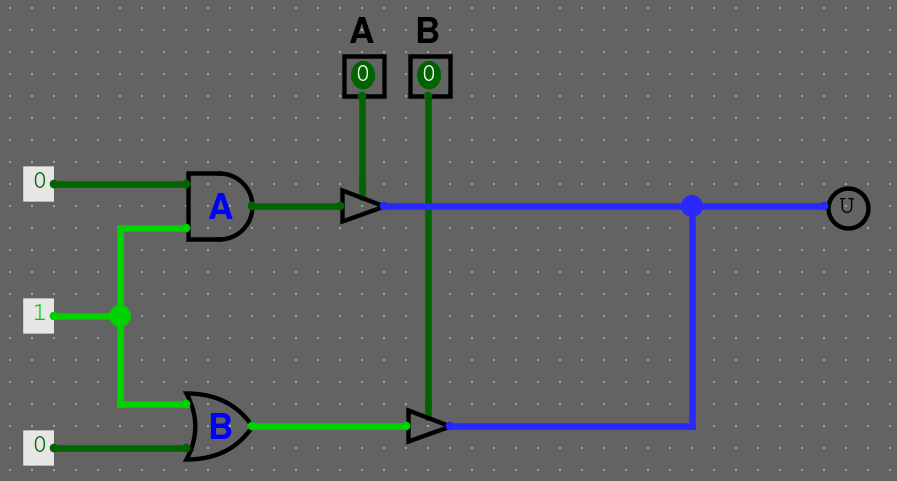
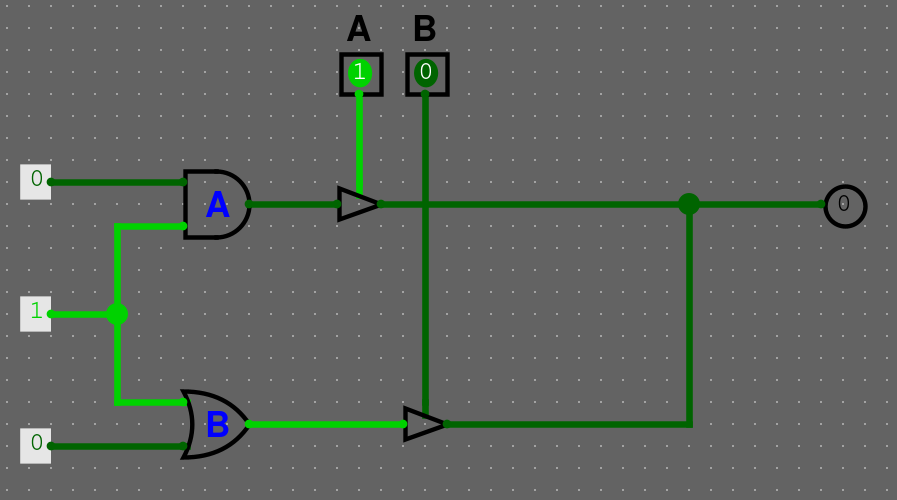
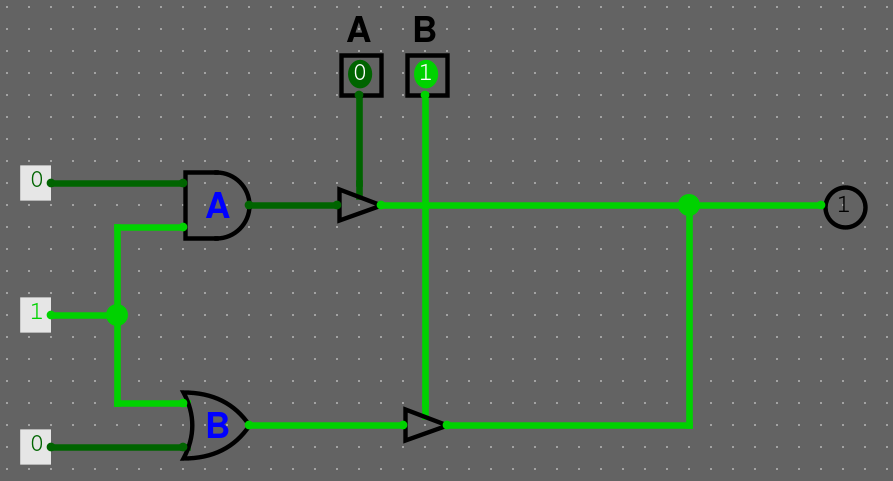
Pokud pustíme vstup A, tak dostaneme 0, pokud pustíme vstup B, tak dostaneme 1.
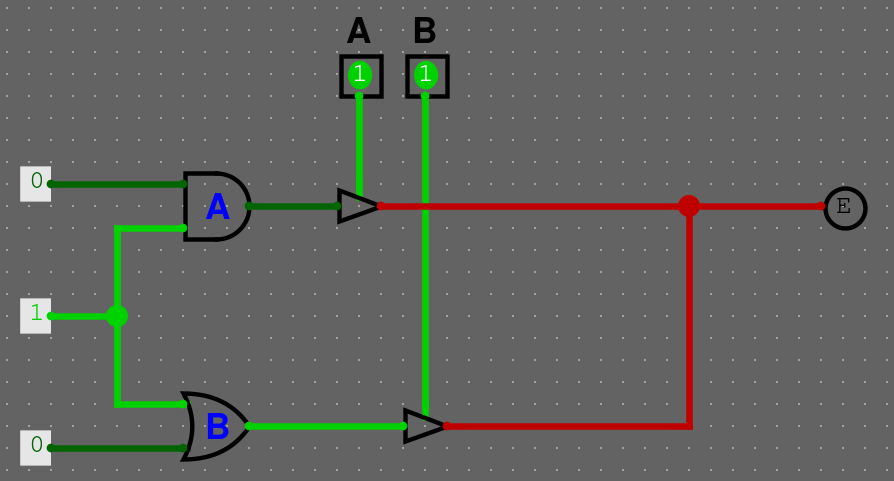
A pokud pustíme oba vstupy na jednou, dostaneme zkrat, jelikož se hodnoty liší.
Multiplexory a dekodéry
Reprezentace čísel jako binární řetězce
Čísel (zatím kladných, později celých) je nekonečno, a jsou to abstraktní objekty. Aby s nimi šlo pracovat, je potřeba je umět nějak vyjádřit. My, lidé, na to používáme desítkovou soustavu, zapíšeme např. číslo 137. Počítače pracují pouze s 0 a 1, takže tato reprezentace není vhodná. Je potřeba zvolit nějakou jinou.
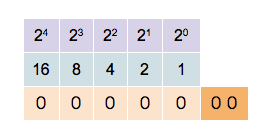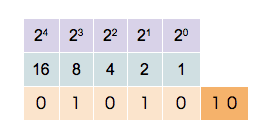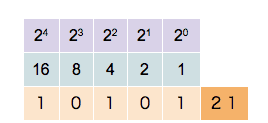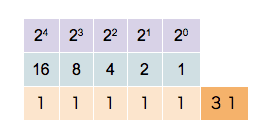
Dvojková soustava
Přirozeně se nabízí použít dvojkovou soustavu neboli binární kód. Číslo reprezentujeme jako součet mocnin dvou (namísto 10 v desítkové). Tento způsob má maximální využití bitů pro přenos informace, tj. pro čísla dané velikosti je nejkratší. Pro reprezentování čísla potřebujeme bitů.
https://commons.wikimedia.org/wiki/File:Binary_counter.gif
Není to ale jediný způsob, jak pomocí řetězce bitů reprezentovat číslo. S několika dalšími způsoby se ještě setkáme, jakmile začneme potřebovat umět reprezentovat záporné čísla. Prozatím ale zůstaneme u čísel kladných.
Kód "1 z N" (one-hot coding)
Kód 1 z N spočívá v zakódování čísla o z rozsahu jako řetězec bitů, kde všechny bity jsou , pouze jediný -tý bit je :
Tento kód je velmi neefektivní z hlediska potřebného počtu bitů, takže v tomto kódu asi nebude nic nikam posílat, ale je velmi užitečný lokálně v obvodech, protože každý bit kódu přesně vyjadřuje, jestli se jedná o dané číslo. Zároveň máme garantované, že pokud je jeden z bitů , všechny ostatní musí být (jinak by se nejednalo o validní hodnotu v kódu 1 z N). Taková sada bitů se velmi hodí na rozhodování typu "switch":
- Pokud byla v paměti tato instrukce, udělej tohle (pro všechny možné instrukce)
- Na vstupu je ID početní operace. Proveď danou operaci.
- Pokud na vstupu byly tyto 4 hodnoty, udělej tohle, jinak udělej něco jiného (bity lze ORnout)
Dekodér
Dekodér má výstupů a bitový vstup (selector). Provádí převod z -bitového binárního čísla do kódu 1 z , tedy říká v jednoduše zpracovatelné podobě které číslo má na vstupu.
Dekodér může mít ještě vstup ENA (enable). Pokud existuje, a je na jeho vstup přivedena , dekodér má na výstupu samé nuly, což má většinou za efekt vypnutí rozhodovací logiky za ním připojené (nenastala ani jedna z variant). Generuje pak kód "až 1 z N".
Pokud používáte dekodér s enable v Logisimu, ujistěte se, že máte nastavenou možnost "Disabled output" na "Zero". Druhá možnost "Floating" by generovala třetí stav, který je až na výjimky zakázaný!
Multiplexor
Multiplexor bere vstupů a bitový vstup selector (SEL). Výstup má pouze jeden. Může taky obsahovat enable (ENA), který určuje, jestli je součástka zapnutá nebo ne.
Multiplexor se chová jako "výhybka" nebo "switch statement": Na svůj jediný výstup pošle hodnotu z toho (-tého) vstup, který je vybraný na selector vstupu (). Na komponentě je vyznačený 0. vstup a ostatní jsou ve vzestupném pořadí.
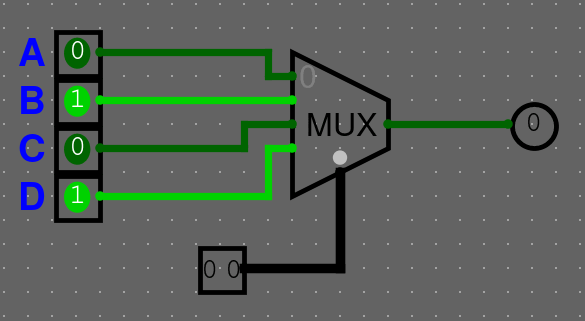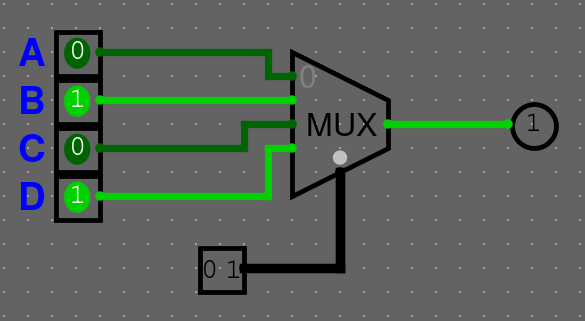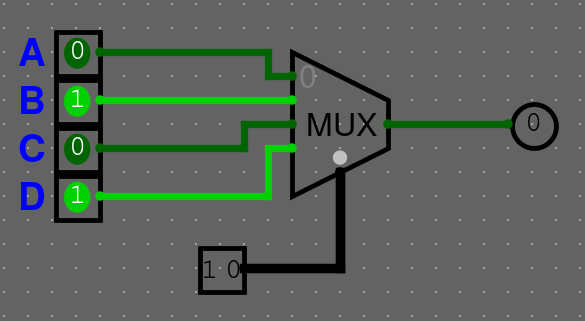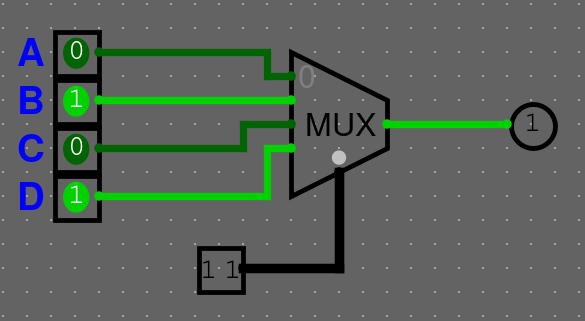
Můžeme si chování multiplexoru shrnout do tabulky
| SEL | Vysílaný vstup |
|---|---|
| 00 | A |
| 01 | B |
| 10 | C |
| 11 | D |
Pro větší multiplexory bude tabulka větší.
Multiplexor může mít kromě "rozhodovací" šířky , která určuje počet vstupů, také "datovou" šířku , která určuje velikost sběrnice každého "kanálu" multiplexoru. Multiplexor pak jednoduše přeposílá -bitové hodnoty ze vstupů na výstup.
Demultiplexor
Demultiplexor se chová obráceně z hlediska vstupů. Má jeden vstup a výstupů.
Pokud má 1-bitový demultiplexor nastavený "Disabled output" na "Zero", chová se stejně (má stejnou logickou funkci a pravdivostní tabulku) jako Dekodér s enable. Datový vstup demultiplexoru pak plní stejnou funkci jako enable u dekodéru.
Cvičení
V kombinačních obvodech je až na výjimky zakázáno používat třetí stav! Každý obvod, pro který by šla vytvořit pravdivostní tabulka, jde postavit ze základních hradel, bez třetího stavu!
Vytvořte si vlastní dekodér, který bude mít 2 bitový SEL vstup.
Vytvořte si vlastní multiplexor, který bude mít 2 bitový SEL vstup a 1 bitové datové bity, pomocí logických bran.
Komparátor
Cvičení
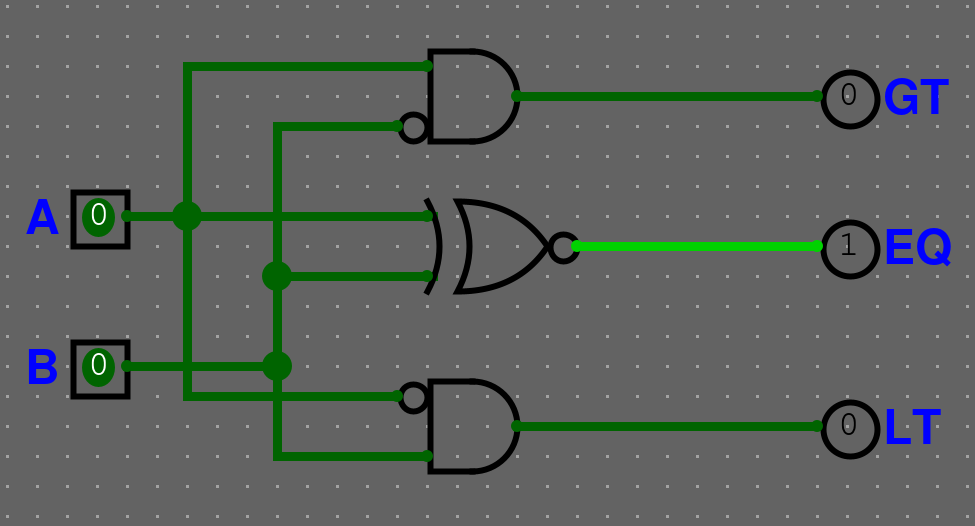
1 bitový komparátor
Postavte 1 bitový komparátor, který má 2 vstupy a 3 výstupy A>B (GT), A=B (EQ), A<B (LT)
Řešení
2 bitový komparátor
Postavte 2 bitový komparátor, který má dva 2 bitové vstupy a 3 výstupy A>B (GT), A=B (EQ), A<B (LT)
Řešení - Komparátor 2b
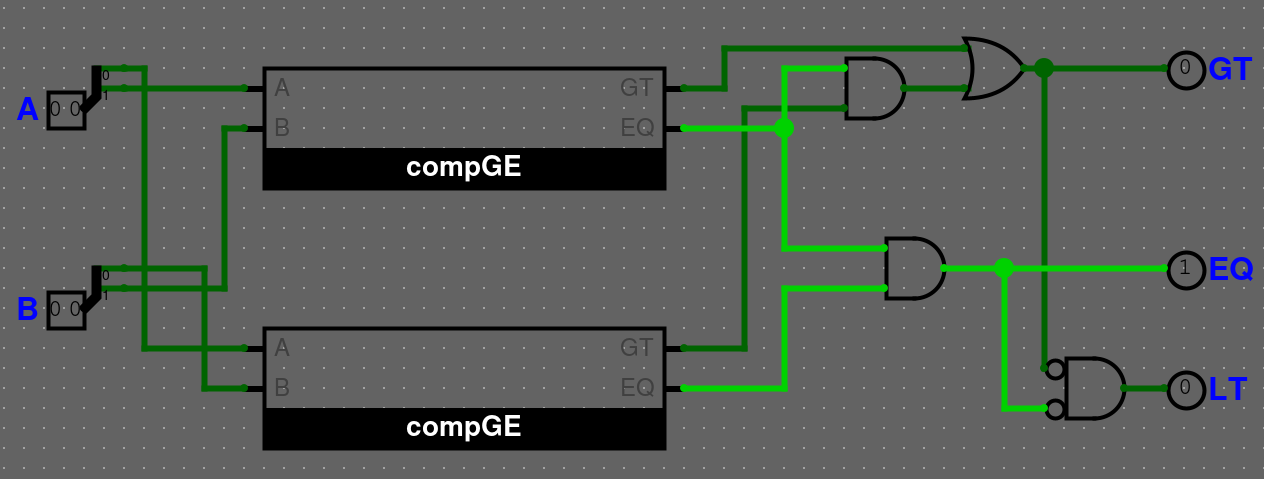
Řešení - compGE
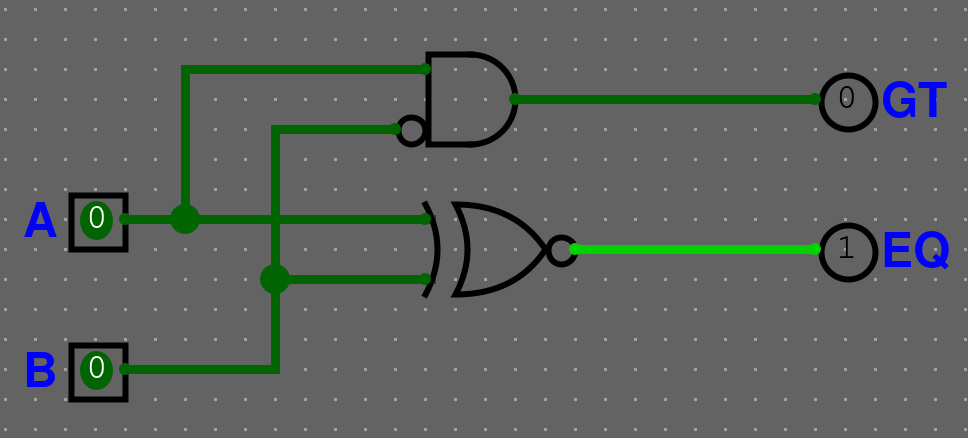
Řešení - Popis
Vytvořili jsme si compGE, abychom ušetřili dvě logic gaty, jelikož potřebujeme pro 2 bitový komparátor pouze GT a EQ.ALU - Úvod
Obsah této stránky slouží jako úvod k principu ALU, má pouze informační povahu a není součástí zadání ALU!
Každé CPU vyžaduje ALU neboli Arithmetic Logic Unit. Jedná se o "krabičku", která dokáže různé operace jako například sčítání, odčítání, bitwise operace, atd... V této kapitole se dozvíte, co je vše potřeba v ALU obsáhnout.
ALU musíte postavit do samostatného modulu, který se musí jmenovat přesně ALU. Jinak nebude možné ALU ohodnotit!
Vstupy ALU
- vstup
AaB- n-bitový vstup, záleží kolika bitové děláte ALU CIN- Carry IN, 1 bitová dodatečná hodnotaSEL- Nebo takyOpcode, typicky 4 bitový, rozhoduje kolik vaše ALU umí operací
Výstupy ALU
OUTP- n-bitový výstup, záleží kolika bitové děláte ALUHOUT- použito pro násobení, využito pro vyšší polovinu výsledkuZERO- 1 bitová hodnota, rozhoduje jestli jsou na výstupu samé nulyCOUT- Carry OUT z operací, 1 bitová hodnotaSIGN- Znaménko hodnoty výstupu (totožné s nejvyšším bitem hodnoty)GT,LT,EQ- Nepovinně můžeme přidat operace z komparátoru, jde nahradit pomocí odčítání aZEROaSIGNvýstupy
Aby bylo možné vaše ALU ohodnotit, je potřeba pro tyto dráty dodržet přesně výše uvedené názvy!
UI (uživatelské rozhraní)
Pro uživatelské rozhraní můžete použít například tyhle logisim komponenty.
Komponenty vstupů
Wiring/Pin- pro 1 bitové hodnotyMemory/Register- pro n bitové hodnotyInput/Output/Button- tlačítko pro například operace
Komponenty výstypů
Input/Output/LED- pro 1 bitové hodnotyWiring/Pin- pro n bitové hodnotyInput/Output/Hex Digit Display- pro 4 bitové hodnoty, doporučuji dost přehledné pro výstup
Příkladný main v projektu ALU může vypadat následovně.

Operace ALU (SEL)
Bitwise operace
Jednoduché logické gaty pro n-bitové vstupy
NOTORANDXOR
Shifty
Posune nám hodnotu buď doleva SHL, nebo doprava SHR. Pokud by hodnota utekla, tedy například na hodnotu 1000 0000 budeme chtít použít operaci SHL, tak rozsvítíme COUT na 1 a OUT bude 0000 0000.
SHL- Shift leftSHR- Shift right
Příklad SHL
| A | OUT | COUT |
|---|---|---|
0000 0001 | 0000 0010 | 0 |
1000 0000 | 0000 0000 | 1 |
1011 0111 | 0110 1110 | 1 |
0101 1101 | 1011 1010 | 0 |
Příklad SHR
| A | OUT | COUT |
|---|---|---|
0000 0001 | 0000 0000 | 1 |
1000 0000 | 0100 0000 | 0 |
1011 0111 | 0101 1011 | 1 |
0101 1101 | 0010 1110 | 1 |
Rotace
Stejné jako shifty, ale při přetečení nastavíme nejmenší hodnotu na 1. Například máme hodnotu 0000 0001 a použijeme operaci ROTR, tak nastavíme OUT na 1000 0000 a označíme COUT na 1
ROTL- Rotate leftROTR- Rotate right
Příklad ROTL
| A | OUT | COUT |
|---|---|---|
0000 0001 | 0000 0010 | 0 |
1000 0000 | 0000 0001 | 1 |
1011 0111 | 0110 1111 | 1 |
0101 1101 | 1011 1010 | 0 |
Příklad ROTR
| A | OUT | COUT |
|---|---|---|
0000 0001 | 1000 0000 | 1 |
1000 0000 | 0100 0000 | 0 |
1011 0111 | 1101 1011 | 1 |
0101 1101 | 1010 1110 | 1 |
Sčítačka
Sčítačka by měla být schopna provést více operací, jedná se o následující.
ADD- sčítáníSUB- odčítáníINC- inkrement (A + 1)DEC- dekrement (A - 1)
Násobení
Bonusově můžete dodělat násobení neboli MUL. Zde se výsledek rozděluje na dva výstupy a to horní část HOUT a dolní část OUT.
MUL- násobení
ALU - Sčítačka/odčítačka
Sčítačka je podstatná část ALU. Po určitých úpravách z ní můžeme udělat dokonce i odčítačku. Začneme jednoduše, a to s jedno bitovou verzí.
Half-adder (1 bit adder)
Pravdivostní tabulka pro half-adder vypadá následovně.
Pomocí karnaughovy mapy nebo i logiky (odkoukání) můžeme zjistit, že sčítání (OUT) je vlastně XOR a COUT je jenom AND. Takže half-adder vypadá následovně.
Full-adder
Full-adder využívá half adder a pomocí něj přijímá další argument a to CIN, neboli carry in.
Pravdivostní tabulka pro full-adder vypadá následovně.
Jediné, co tedy uděláme je, že přidáme half-adder 2 krát, jeden na A+B a druhý na výsledek z prvního X a CIN, neboli X+CIN.
COUT half-adderů by se měly sčítat, ale jelikož nemůže nastat případ, kdy jsou oba dva COUT 1, tak nám stačí OR. Taky se nemusíme bát přetečení, jelikož při sčítání 3 bitů se hodnota vždy vejde do 2 bitů (maximální hodnota je 3).
Binární odčítačka
Odčítání jako sčítání
Sice lze postavit dedikovaný obvod, který umí odečíst dvě čísla, podobným postupem jako u sčítačky, akorát podle odčítání pod sebou.
Nicméně o odčítání se dá uvažovat jako o přičítání záporných čísel, v matematice je to běžná věc.
Pokud bychom tedy byli schopní vytvořit nějaký jednoduchý obvod, který z umí vytvořit nějakou hodnotu , kterou můžeme přičíst k , abychom dostali , můžeme pro odčítání použít naši existující sčítačku.
Záporná čísla
Číslu z předchozího příkladu budeme říkat zaporné číslo. Samozřejmě se pořád pohybujeme v digitální logice, toto číslo bude v počítači muset být reprezentované nějakou sekvencí a . Způsobů, jak to udělat, je hned několik (stejně jako u kladných čísel jsme měli binární kód, Grayův kód a BCD), a každá reprezentace bude mít své výhody a nevýhody.
V každém případě předpokládáme, že šířka našeho čísla v bitech je konstantní, protože naše sčítačka/ALU/CPU bude umět pracovat vždy s přesne -bitovými čísly.
Přímý kód (sign-magnitude)
Asi nejjendodušší, co vás napadne, je do jednoho z bitů (zpravidla největšího) "prostě" uložit znaménko zakódvané jako nebo , a zbytek bitů interpretovat jako normální číslo.

Tato reprezentace má několik nevýhod, zejména:
- Pro sčítání těchto čísel je potřeba speciální sčítačka, zčásti protože:
- Máme dvě různé nuly, a , tedy i porovnávání čísel je komplikovanější
- Odčítání nelze realizovat jednoduše jako přičtení záporného čísla
Aditivní kód (offset binary)
Další přirozený způsob spočívá v posunutí nuly "doprostřed" reprezentovatelného rozsahu - směrem nahoru budou kladná, směrem dolů záporná. Tedy v případě 8-bit čísel, kde máme 256 různých čísel, můžeme dát nulu na číslo , takže bude a bude .
Jedná se v podstatě o přímý kód, ale s opačným významem bitu znaménka, má stejné nevýhody.
Jedničkový doplňěk (one's complement)
Další dva možné způsoby reprezentace spočívají v hledání opačných prvků ke kladným číslům pomocí nějakého vzorce. Nejjednodušší takový vzorec je najít záporné číslo pomocí bitwise negace.
Tedy bude a . Protože je , bude , a podobně.
Tento kód má zase podobné nevýhody.
Dvojkový doplněk (two's complement)
Pojďme zkusit vymyslet takový kód, který bude mít vhodnou reprezentaci záporných čísel, abychom odstranili nevýhody ostatních kódů. Tedy chceme mít pouze jednu nulu, chceme aby kladné čísla měla stejnou reprezentaci jako bez znaménka, a chceme, aby šlo odčítat přičtením záporného čísla:
Když pracujeme s n-bitovými čísly, tak vlastně pracujeme s groupu , protože hodnoty a větší neumíme reprezentovat a horní bity zahazujeme (carry).
Např. sčítáme 8-bit čísla, pohybujeme se v :
Chceme označit některá čísla z této grupy jako záporná tak, aby platily následující pravidla:
- Pro každé kladné (které reprezentujeme jako číslo bez znaménka) musí existovat takové , aby platitlo .
- To je ekvivalentní tvrzení
Hledané je tedy aditivní inverzí v . Tu umíme aritmeticky najít:
Pokud toto pravidlo budeme aplikovat na nezáporná čísla počínaje nulou (která je korektně sama svojí vlastní inverzí), začneme záporným číslům přiřazovat reprezentace. Přestaneme, jakmile nám dojdou volná čísla (číslo, které jsme označili jako záporné už nemůžeme zároveň považovat za kladné). Pro n=3 skončíme s následujícím přiřazením:
| Binární řetězec | Bez znaménka | Dvojkový doplněk? |
|---|---|---|
000 | 0 | 0 |
001 | 1 | 1 |
010 | 2 | 2 |
011 | 3 | 3 |
100 | 4 | 4 nebo -4 ? |
101 | 5 | -3 |
110 | 6 | -2 |
111 | 7 | -1 |
Tento kód ja zajímavý tím, že není nemá symetrický rozsah, tedy stejný počet kladných a záporných čísel. To vyplývá automaticky z požadavku mít pouze jednu nulu, přičemž čísel je pořád sudý počet. "Lichý" binární řetězec můžeme přiřadit buď číslu nebo , výsledný kód bude fungovat stejně, protože nad platí, že . Vlastně tedy (stejně jako pro nulu), platí, že .
Tvoří prvky dvojkového doplňku a sčítání stále grupu?
Tvoří prvky dvojkového doplňku a sčítání stále grupu?
Ano, pouze jsme prvkům dali jiné názvy. Operátor nad nimi se chová pořád stejně jako v původním . Mezi sčítáním čísel bez znaménka a ve dvojkovém doplňku není na binární úrovní žádný rozdíl. To znamená, že pro sčítání čísel ve dvojkovém doplňku můžeme používat stejnou sčítačku, jako pro nezáporná čísla!
Musíme se tedy při tvorbě kódu rozhodnout, jestli chceme více záporných a více kladných čísel, aby šly čísla jednoznačně interpretovat. Pokud se rozhodneme "lichému" řetezci přiřadit zápornou hodnotu, získáme pro nás kód navíc jednu velmi hezkou vlastnost:
| Binární řetězec | Bez znaménka | Dvojkový doplněk |
|---|---|---|
0 00 | 0 | 0 |
0 01 | 1 | 1 |
0 10 | 2 | 2 |
0 11 | 3 | 3 |
1 00 | 4 | -4 |
1 01 | 5 | -3 |
1 10 | 6 | -2 |
1 11 | 7 | -1 |
Nejmohutnější (most significant) bit binárního řetězce ve dvojkovém doplňku přímo odpovídá znaménku čísla!
Tomuto kódu, jak jsem jej teď sestavili, se říká dvojkový doplněk nebo doplňkový kód, a používá jej drtivá většina architektur a jazyků pro reprezentaci záporných čísel.
Rozdělili jsme tak grupu na dvě stejně velké poloviny: zápornou a nezápornou:
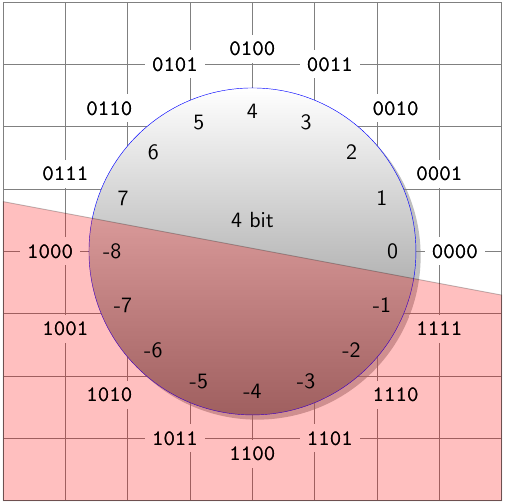
Konkrétní příklad
Co se vlastně na pozadí děje, když odečteme pomocí této techniky nějaké číslo?

Pracujeme s 4-bitovými čísly, tedy (bez znaménka) v . Se znaménkem pracujeme v doplňkovém kódu ona obrázku.
Chceme spočítat . Nalezneme opačnou hodnotu pro číslo :
Výsledek můžeme oveřit na obrázku. Takže z našeho příkladu se stane:
Získali jsme správný výsledek. Pozorujeme, že odčítání vlastně funguje pomocí přičtení "velkého" čísla, což způsobí přetečení o "tak akorát" velké číslo, abychom dostali správný výsledek. Znamená to, že carry-out už nám bohužel nemůže nic říct o tom, zda je výsledek validní.
Lze spočítat absolutní hodnotu z libovolného čísla ve dvojkovém doplňku?
Lze spočítat absolutní hodnotu z libovolného čísla ve dvojkovém doplňku?
Ne bez zvětšení počtu bitů. Pro 3-bitové číslo :
ale lze reprezentovat pouze ve 4- a více-bitových číslech.
Je to opravdová situace, která může nastat ve strojových číslech se znaménkem:
fn main() { let min = std::i8::MIN + 1; // -128 + 1 = -127 println!(" min: {}", min); println!("|min|: {}", min.abs()); }
fn main() { let min = std::i8::MIN; // -128 println!(" min: {}", min); println!("|min|: {}", min.abs()); }
Validita výsledku, přetečení (carry) a přeplňení (overflow)
U sčítání jsme měli výstup carry, který nám indikoval, že výsledek se nevejde do šířky výstupu sčítačky. Tomu jevu se říkalo přetečení.
U záporných čísel se to trochu komplikuje - jak jsme si ukázali na příkladu, zde nám carry může a nemusí nastat ikdyž je výsledek validní. Tedy "přetečení" neboli carry nám nepomůže.
Potřebujeme vymslet jiný indikátor toho, jestli operace ve dvojkovém doplňku byla validní. Pokud tomu tak nebude, budeme tomu říkat přeplňení (overflow).
Přeplnění nastane, pokud hodnota "vyjede" z reprezentovatelného rozsahu. U čísel se znaménkem to může být směrem nahoru (mělo vyjít číslo vyšší, než to nejvyšší reprezentovatelné) nebo směrem dolů (menší než nejmenší reprezentovatelné).

Danou operací sčítaní nebo odčítání se můžeme na kruhu posunou pouze o půlkruh. Tedy, pokud se budeme pohybovat směrem k nule, musíme garantovaně skončit v druhé půlce kruhu, a naše odpověď bude validní. Např. pokud jsme v záporných číslech a přičítáme, skončíme nejdál o půlkruh dál v kladných číslech, na správném výsledku.
Pokud tedy sčítáme kladné a záporné číslo, nemůže přeplnění nastat.
Problém nastává, pokud máme záporné číslo a chceme dále odečítat, nebo máme kladné číslo a chceme dále přičítat. Tedy, přeloženo pouze na součty, máme záporné číslo a chceme přičíst záporné číslo, nebo máme kladné číslo, a chceme přičíst kladné číslo. Tam by se mohlo stát, že se přehoupneme přes hranici MIN-MAX, a číslo náhle změní polaritu.
Tedy, pokud sčítáme kladné a kladné číslo, musí být výsledek kladný, aby byl validní.
Podobně, pokud sčítáme záporné a záporné číslo, musí být výsledek záporný.
Jak víme, znaménko je u čísel se znaménkem vždy Most Significant Bit hodnoty, můžeme tedy sestavit pravdivostní tabulku pro vyhodnocení overflow:
| A | B | A+B | Overflow? |
|---|---|---|---|
| + | - | X | 0 |
| - | + | X | 0 |
| + | + | + | 0 |
| + | + | - | 1 |
| - | - | - | 0 |
| - | - | + | 1 |
Tento signál si pojmenujeme overflow a vyvedeme taky z ALU, podobně jako cout, bude užitečný procesoru v rozhodování o validitě operací se znaménkem.
Efektivní hledání opačného čísla ve dvojkovém doplňku
Našli jsme tedy pěkný kód, který nás nechá pro odčítání recyklovat naši existující sčítačku. Ale, abychom doopravdy mohli odčítat, musíme být schopni rychle nalézt k danému číslu jeho opačné číslo.
Vzorec pro opačné číslo v doplňkovém kódu je následující:
...ovšem pro výpočet tohoto vzorce musíme umět odčítat. Je potřeba se tohoto odčítání nějak "zbavit" a nahradit ho jinou operací, kterou spočítat umíme.
S trochou algebry získáme:
v tomto výrazu je konstanta, která má podobu binárního řetězce samých jedniček o délce . Odečtením libovolného čísla od takové hodnoty nikdy nenastane žádný přenos a odečítaná hodnota se touto operací jednoduše zneguje (vyzkoušejte odečtením pod sebou na papíře), tedy . Dosazením do původního vzorce dostáváme
což je vzorec pro efektivní výpočet opačného čísla ve dvojkovém doplňku v hardwaru. Pozor, pokud je dvojkový doplňěk n-bitový, musí i negace být n-bitová!
Tedy, pokud chceme odečíst dvě čísla A, B, stačí provést:
Pokud chceme odčítat, přivedeme tedy na vstup B naší odčítačky invertovanou hodnotu. Na první pohled se zdá, že budeme muset provést dva součty, nicméně lze na naší sčítačce zajistit pomocí vstupu cin, který při odčítání zafixujeme na kostantní 1.
Z poloviční odčítačky na úplnou
Tím, že jsme takhle použili cin, jsme znemožnili řetězení více menších rozdílů pro provedení většího, jako to šlo u sčítání. Hovoříme tedy o poloviční odčítačce (half-subber). Jak tedy tuto funkcionalitu obnovit, a získat plnou odčítačku (full-subber)?
U odčítání se řetězení provádí pomocí tzv. výpůjčky (borrow). Pokud je borrow-in , odečteme ještě o jedničku více (podobné ale opačné chování jako carry). Na výstupu odčítačky je naopak borrow-out, který signalizuje přetečení do záporných hodnot, tedy v dalším řádu se má odečíst jednička navíc (borrow-in).
Pokud do našich výpočtů zahrneme borrow-in ():
lze podobně jako předtím vyjádřit jako . Máme tedy:
Tuto operaci opět provedeme na naší sčítačce, jako cin při odčítání přivedeme . borrow-in je tedy pouze invertované carry-in.
Kvůli neuvedeným skutečnostem (doplňkový pseudokód) platí to samé pro borrow_out:
Tedy abychom dostali borrow_out pro odčítání, stačí znegovat carry_out z výše uvedeného součtu.
Obecně tedy platí, že carry u sčítání a borrow u odčítání jsou přesné opaky. Tedy pokud převádíme odčítání na sčítání, je potřeba převést borrow-in na carry-in, provést součet, a poté převést výsledný carry-out na borrow-out.
V ALU bude typicky pouze jeden carry-in a jeden carry-out výstup. Tyto IO mají pak dvojí smysl, během sčítání zastávají funkci carry, a během odčítání borrow.
Sčítačka-Odčítačka
ALU musí samozřejmě umět nějěnom odčítat, ale i sčítat. Nestačí tedy zkonvertovat sčítačku na odčítačku. Taky není dobré řešení mít dvě sčítačky, jednu na sčítání a odčítání, když ALU děla v jeden čas vždy pouze jednu z obou operací, to je v ALU penalizováno.
Je tedy potřeba postavit modul sčítačka-odčítačka, který umí obojí, a má speciální vstup (může se jmenovat např. sub jako subtract), kterým lze zapnout režim odčítání.
- V režimu sčítání bude počítat .
- V režimu odčítání bude počítat (varianta
half_sub)- Tedy se nebere v potaz, výstup je zapojen stejně jako u součtu.
- Alternativně v režimu odčítání bude počítat (varianta
full_sub)- mají korektní borrow chování ve dvojkovém doplňku, viz "Jak zřetězím dve odčítání"
- je jeden vstup pojmenovaný
CINneboCIN_BIN, který přepíná své chování podle toho, zda se zrovna odčítá. - stejně.
Implementace
Pro implementaci této komponenty je samozřejmě potřeba mít jako modul hotovou sčítačku. Poté stačí pomocí vhodných multiplexorů podle vstupu sub vybírat, jaké hodnoty vlastně na vstupy sčítačky chceme přivést, případně jaké hodnoty (třeba vypočtené z výstupů sčítačky) chceme vyvést na výstupy modulu.
Zadání projektu ALU
Vytvořte v Logisim Evolution modul tzv. Aritmeticko-Logické jednotky (ALU). ALU je (v našem provedení) kombinační obvod, který umí provést vždy jednu vybranou z několika podporovaných aritmetických nebo logických operací.
Formální náležitosti odevzdání
Odevzdání
Odevzdávání probíhá na platformě Submitty hostované mnou na adrese: https://submit.vojacek.org. Pro přihlášení potřebujete přihlašovací údaje, které jste dostali automatizovaným emailem (zkuste se podívat i do spamu, a email ze spamu přesuňte do doručených, aby se vám nesmazal!). Více informací naleznete právě v tomto emailu. V případě problémů mě kontaktujte emailem.
V případě, že by systém nefungoval, je záložní metoda odevzdání emailem. V takovém případě odevzdáváte vždy přímo v příloze zip archiv pojmenovaný alu_{jmeno}_{prijmeni}_{cislo odevzdani}.zip. Odkazy na OneDrive atp. nejsou přípustné, protože jejich obsah lze upravit po odevzdání. Projekt ALU se bez problému vejde přímo do emailu.
Soubory odevzdání
| Název souboru | Popis |
|---|---|
| ALU.circ | Projektový soubor Logisimu obsahující ALU |
| *.circ | Libovolné další .circ soubory nutné pro funkčnost ALU |
| OPCODES.txt | Strojově čitelný popis operačních kódů implementovaných v ALU |
| Dokumentace.xlsx/.ods | Uživatelsky přívětivá dokumentace ALU |
| README.md | Jakékoliv další připomínky k odevzdání |
Je potřeba dodržet přesné názvy souborů, včetně kapitalizace! ALU budu vyhodnocovat částečně strojově, v případě špatně pojmenovaných souborů nepůjde ohodnotit.
Projekt v Logisimu
- Použijte Logisim Evolution 4.0.0
- Modul ALU v Logisimu se musí jmenovat
ALU. Pokud ho máte jiný, vytvořte správně pojmenovaný modul a překopírujte obsah (Ctrl-A, Ctrl-C, Ctrl-V). - Všechna dvou-vstupová hradla musí mít velikost Narrow, pokud není vyloženě vhodné mít jinou. Doporučuji použít template.
- Všechny moduly mají pojmenované všechny vstupy a výstupy vhodným jménem.
- Používání třetího stavu (a jej generující komponenty) je obecně zakázáno. U každého použití je nutné odůvodnit (text toolem v logisimu v místě použití), proč je to vhodné místo klasických hradel a že nenastává žádný z problémů obecně spojeným s třetím stavem.
- V ALU je dovoleno je používat následující komponenty z knihoven:
- Wiring: Splitter, Pin, Probe, Tunnel, Constant
- Gates: NOT, Buffer, AND, OR, NAND, NOR, XOR, XNOR
- Pro postavení modulu ALU by neměly být žádné jiné komponenty potřeba. V případě nejasností se ptejte. Mimo modul ALU můžete použít libovolné komponenty - např. pro testování, ukázku, etc.
- V ALU je pouze jedna instance 16-bit sčítačky. Všechny operace, které ji potřebují, se na ní musí vystřídat, ALU provádí pouze jednu operaci zároveň. Použití více sčítaček je penalizováno jako hrubá neefektivita zapojení.
Pro implementování bonusových operací jsou tyto restrikce rozvolněné. Např. uvnitř násobičky můžete použít vestavěnou sčítačku, čímž se zásadně zrychlí simulace obvodu. Dokonce to doporučuji. Nemůžete ale např. pro implementaci násobičky použít logisimovou násobičku.
- V modulu
main,alu_main,alu_showcasenebo podobně bude implementovaná showcase vašeho ALU:- Je zde položený váš ALU modul
- Všechny vstupy jsou odvozené z komponent, kterým lze jednoduše upravovat hodnota v decimal nebo hexadecimal (např. input pin se správně nastaveným radixem)
- Všechny výstupy jsou napojené na komponenty, na kterých je srozumitelně vidět jejich hodnota (opět decimal nebo hexadecimal) (např. LED, output pin se správně nastaveným radixem)
- Radix (soustava, e.g. decimal nebo hexadecimal) všech vstupů a výstupů je stejný
Dokumentace.xlsx
Každý číslicový modul (v praxi se používá zkratka IP znamenající Intellectual Property) musí mít detailní dokumentaci, často jsou to dokumenty o desítkách až stovkách stran.
Interní dokumentace slouží pro zorientování v implementaci modulu a navázání na vývoj po delší době nebo po kolegovi. Tu u ALU vynecháme.
Externí dokumentace dokumentuje interface (vstupy a výstupy) modulu, jeho operační režimy, chování, zakázané kombinace vstupů, případně elektrické vlastnosti. U nás jako 90% externí dokumentace slouží toto zadání - vstupy, výstupy a chování jsou tu přesně popsané. Je ale potřeba zdokumentovat hodnoty vstupu SEL, které jsou plně ve vaší režii.
Pro tento účel jako součást odevzdání ALU vypracujete soubor Dokumentace.xlsx (nebo .ods), ve kterém tohle chování popíšete. Formát a obsah dokumentace není striktně definovaný, ale měl by pro každou implementovanou operaci obsahovat v přehledné podobě alespoň následující informace:
- Hodnotu SEL v desítkové soustavě (jako v OPCODES.txt)
- Binární rozvoj SEL s obravenými buňkami. Bity uspořádejte tak, že MSB bude vlevo.
- ID operace
- Mnemoniku krátce vystihující chování operace (příklady máte uvedené ve sloupci
Mnemov tabulkách a v obrázku níže. Není tu správná a špatná odpověď, stačí si vymyslet krátký "assemblerový" způsob, kterým by mohl programátor tuto operaci chtít použít v programu. Důležité je pouze, aby vámi zvolený styl byl konzistentní napříč celou ALU dokumentací) - Stručný slovní popis operace (e.g. Sečte A, B a CIN. Výsledek je OUTP, COUT. Spočítá OVER, ZERO, SIGN.)
Pro automatické podbarvení buněk s binárním rozvojem můžete použít podmíněné formátování. Na použítých stylech nezáleží, stačí, aby byly odlišné.
Tyto údaje má smysl formátovat do tabulky (proto xlsx), a takové tabulce nesmí chybět hlavička. Obzvlášť u binárního rozvoje je vhodné označít číslo každého bitu, případně MSB a LSB (Most- a Least-Significant-Bit).
Příklad dokumentace:

OPCODES.txt
Soubor OPCODES.txt je strojově čítelnou verzí dokumentace, která slouží pro automatizovaný opravovač, aby věděl, jaké operace jste implementovali a jak je nechat ALU spočítat. Je to CSV bez hlavičky s řádky ve formátu {opcode},{ID}, např.
0,and
1,or
2,not
3,cla
15,mul8
opcode je zde číslo, které se přívádí na vstup SEL, zapsané v desítkové soustavě. "opcode" je zkratka pro operation code, neboli číslo identifikující operaci.
ID je ID operace, jak je uvedené ve sloupci ID v tomto zadání, nebo custom jako označení oprace, která není v zadání (pro vyjímečné případy, kdy chcete naimplementovat nějakou jinou operaci navíc za bonusové body).
V případě použití custom budu danou operaci hodnotit ručně, je tedy potřeba, aby byla detailně popsaná v dokumentaci ALU.
Na pořadí nezáleží, a v souboru nesmí být žádné jiné údaje. Sada popsaných operací musí být konzistentní s dokumentací!
Plagiáty
Všechny projekty v předmětu APS jsou samostatné práce, musí tedy produktem vaší vlastní práce. Je povoleno projekty probírat, konzultovat, nechat si pomoct s řešením problému. Je nepřípustné odevzdávat cizí práci, a to včetně případů, kdy jste obvod podle předlohy zapojili sami.
Ve skriptech a na internetu je dostatek informací pro řešení projektu, je nutné danou problematiku pochopit.
Do výsledného hodnocení se bude vždy započítávat pouze vaše vlastní práce. V případě porušení budou uděleny nevratné záporné body.
Hodnocení
Hodnocení ALU je rozloženo do průbežného plnění domácích úkolů o komponentách ALU (10b) a do odevzdání samotného hotového ALU (10b).
V samotném ALU se hodnotí:
- správnost všech povinných operací (4b)
- provedení a vzhled zapojení (3b)
- správnost a úprava dokumentace (3b)
Pokud jsou všechny části vyjímečně kvalitně zpracovány, může být udělen 1 bonusový bod.
Dále je možné získat až 6 bonusových bodů za bonusové operace, ale pouze pokud povinná část ALU byla ohodnocena plnými 10b.
Časté problémy
- Absence povinné části odevzdání (dokumentace, prohlášení, etc.) (= 0 bodů)
- Použití zakázaných komponent (= 0 bodů)
- Errory, zkraty, třetí stav (= 0 bodů)
- Nezapojené (floating) vstupy do komponent (-1 bod za zapojení)
- Nesmyslné zapojení (podle závažnosti)
- Překrývající se dráty a/nebo komponenty (-1 bod za zapojení)
- Nikam nevedoucí (zbytečné) dráty nebo komponenty (-1 bod za zapojení)
- Použití více než jedné sčítačky (= 0 bodů za zapojení)
- Drobná neefektivita, např. (-1 bod za zapojení)
- Porovnávání s konstantou pomocí (drahého) obecného komparátoru
- Zbytečné operace na velkých (např. 16bit) hodnotách
- U BCD: použití sčítačky a komparátoru místo zjednodušeného obvodu
- U CLA: přítomnost kritické cesty, která je řádově odpovídá šířce sčítačky (nedošlo ke zrychlení sčítání)
Za neefektivitu se nepovažuje:
- Zbytečné operace na 1bit hodnotách - jsou zanedbatelné
- Použití vícevstupového multiplexoru, kde více vstupů ma stejnou hodnotu (stejný vodič), nebo jsou to konstanty - tyto případy lze velmi jednoduše mechanicky zjednodušit, a tak s tím počítáme
- Ale pozor na to, že při použití takového multiplexoru musí být všechny vstupy zapojené!
- Zapojení, které sice lze zjednodušit, ale jeho aktuální podoba byla explicitně navržena tak, aby bylo patrné, jak obvod funguje (pro přehlednost, atd.)
Automatická kontrola některých problémů
Zadání ALU je zadefinované tak, aby šlo ALU nasadit na FPGA. Pokud by tomu něco bránilo, nejspíš jsou za to body dolů. Zkontrolovat "nasaditelnost" a tím pádem i některé náležitosti vašeho obvodu můžete tak, že necháte Logisim vygenerovat z vašeho modulu HDL, což je zdrojový kód pro popis obvodů. Logisim během toho kroku spustí tzv. Design Rule Checking (DRC), který kontroluje např:
- Nezapojené vstupy modulů
- Zkraty
- Splittery nenapojené na žádnou sběrnici
- K ničemu nepřipojené dráty
- Dráty s nějakou hodnotou (sources) které nejsou připojené k něčemu užitečnému (sinks). Tohle varování nebrání syntéze pro FPGA a nemusí vadit, pokud nejde o extrém.
Návod
- Uložte nebo zazálohujte svůj projekt, tímto procesem ho částečně poškodíte
- Otevřete modul ALU
- V horní liště: FPGA -> Synthetize & Download
- V nově otevřeném okně:
- Tlačítko "Annotate": vygeneruje náhodné labely všude kde je potřeba (odteď projekt neukládejte)
- Jako "Target Board" vyberte třeba "BASYS3", je to docela jedno
- Ujistěte se, že v "Toplevel:" je vybraný modul "ALU", jinak ho vyberte
- Mezi "Toplevel:" a tlačítkem "Execute" vyberte "Generate HDL only" místo "Synthetize & Download"
- Stiskněte "Execute"
- Pokud se zobrazí okno "Component to FPGA board mapping", nic závažného nebrání vašemu projektu v konverzi na HDL a následnému nasazení na FPGA
- Pokud ne, budou ve spodní části okna nejaké Errory a/nebo Warningy
- V obou případech se podívejte do "Warnings" a "Errors" a vyhodnoťte závažnost problému
- Na záznamy lze klikat, což vás přesune na místo, kde varování vzniklo
- Okno nebrání v používání Logisimu, můžete ho nechat otevřené
- Poznamenejte si bokem, co všechno je potřeba opravit
- Zavřete Logisim bez uložení, abyste zahodili změny způsobene krokem "Annotate"
Vstupy a výstupy (I/O) ALU
Naše ALU je 16-bitové, to znamená že umí zpracovat data (čísla) o šířce 16 bitů. Z toho vyplývá, že všechny vstupy a výstupy, kterými tečou data (čísla), musí mít 16 bitů.
| Název v Logisimu | I/O | Šířka | Popis funkce |
|---|---|---|---|
A, B | IN | 16 | 16-bitové vstupy do ALU |
CIN | IN | 1 | Vstup carry-in (borrow-in) pro některé ALU operace (+, -, posuny, ...) |
SEL | IN | 4 | Vybírá aktuálně prováděnou operaci v ALU |
OUTP | OUT | 16 | 16-bitový výstup z ALU |
HOUT | OUT | 16 | Horní polovina výsledku, pokud je výsledek operace širší než 16 bitů (např. násobení 16bit x 16bit) |
COUT | OUT | 1 | Výstup carry-out (borrow-out) pro některé ALU operace (+, -, posuny, ...) |
ZERO | OUT | 1 | Indikuje, že OUTP je roven 0 |
SIGN | OUT | 1 | Indikuje, že OUTP, pokud ho interpretujeme ve dvojkovém doplňku, je záporné číslo |
OVER | OUT | 1 | V případě, že došlo k součtu, indikuje, že pokud by se operace brala jako ve dvojkovém doplňku, je výsledek nevalidní (nevešel se do reprezentovatelného rozsahu) |
GT, LT, EQ | OUT | 1 | Indikují vztah porovnání mezi A a B nezávisle na aktuálně vybrané operaci. GT se rozumí A > B. |
Ne všechny I/O musí být nutně přítomné, pouze ty, které jsou potřeba pro nějakou z implementovaných operací. Taky je přípustné mít I/O navíc, které slouží nějaké funkcionalitě nad rámec, nebo bonusovým operacím - v takových situacích bude funkcionalita ověřena ručně.
Vstupy a výstupy musí být pojmenované přesně podle tabulky, jinak jejich hodnota nebude při opravování brána v potaz! Modul ALU se musí jmenovat ALU!
Definovanost výstupů a relevance vstupů
Následující tabulka definuje, které výstupy musí být pro danou operaci smysluplně definované (mít hodnotu podle definice operace) a na kterých vstupech hodnota závisí.
Jako rule of thumb platí: každý výstup z ALU by měl být vypočten pomocí aktuálně vybrané operace v ALU, nebo být pokud to nedává smysl.
| ID | Inputy | Outputy |
|---|---|---|
xor, or, and | ||
not | ||
shr, shl | ||
rotr, rotl | ||
add | ||
sub_half | ||
sub_full | ||
inc | ||
dec | ||
mul8 | ||
mul16 | ||
swap8 | ||
bsh | ||
bshl | ||
bshr | ||
| všechny | ||
| binární |
V ostatních případech musí hodnota těchto výstupů být ! Není přípustné, aby na výstupech kdykoliv byl třetí stav, error, nebo náhodná/nerelvantní hodnota.
Operace ALU
Pseudokód
značí assignment, tedy že bity z B se použijí pro konstrukci A (výsledku).
značí konkatenaci, tedy že bity A a B se spojí do širší hodnoty, více důležité bity vlevo. Do takové hodnoty lze i assignovat.
v tomto kontextu značí "pro všechny (indexy bitů)", kromě indexů, pro které operaci nelze provést. Typicky 0..15, což jsou indexy bitů 16-bitové hodnoty, kde index je LSB (Least Significant Bit).
značí slice neboli bitový výběr. V tomto případě vybereme bity 7 až 0, ve výsledné hodnotě budou uspořádané tak, že bit z je nejvíc vlevo (MSB), tedy neměníme pořadí bitů.
Typy operací
| Typ | Význam |
|---|---|
| ‼️ | Povinné a důležité |
| ❗ | Povinné |
| ❓ | ...za určitých podmínek |
| 🤷♂️ | Volitelné |
| 🧑🎓 | Bonusové |
Operace po bitech (bitwise)
| Typ | ID | Mnemo | Pseudokód | Popis |
|---|---|---|---|---|
| ‼️ | xor | A XOR B | XOR A a B po bitech | |
| ‼️ | or | A OR B | OR A a B po bitech | |
| ‼️ | and | A AND B | AND A a B po bitech | |
| ‼️ | not | NOT A | NOT A po bitech |
Více informací na wikipedii: Bitwise operators
Posuny a rotace (shifts and rotations)
| Typ | ID | Mnemo | Pseudokód | Popis |
|---|---|---|---|---|
| ‼️ | shr | SHR A | | Logický posun doprava |
| ‼️ | shl | SHL A | | Logický posun doleva |
| ‼️ | rotr | ROTR A | | Rotace doprava |
| ‼️ | rotl | ROTL A | | Rotace doleva |
Pomocí logických posunů (a správného použití carry) lze rychle provést dělení a násobení dvěma, a to jak u čísel bez znaménka, tak u čísel v doplňkovém kódu.
Shifty
Více informací na wikipedii: Rotate through carry
Rotace
Vice informací na wikipedii: Rotate
Sčítání a odčítání
| Typ | ID | Mnemo | Pseudokód | Popis |
|---|---|---|---|---|
| ‼️ | add | A ADD B | Součet respektující carry | |
| ‼️ ❓ | sub_half | A SUB B | Rozdíl bez borrow | |
| ‼️ ❓ | sub_full | A SUB B | Rozdíl respektující borrow | |
| ❗ | inc | INC A | Zvětšení A o 1 | |
| ❗ | dec | DEC A | Změnšení A o 1 |
Z operací sub_half a sub_full stačí implementovat pouze jednu. V případě volby sub_half bude pomocí ALU obtížné odečítat větší než 16bit hodnoty.
Operace inc a dec neberou v potaz hodnotu CIN a provádějí vždy úpravu o 1!
Operace inc musí správně vygenerovat COUT!
Operace dec nemusí správně vygenerovat COUT (netestuje se).
Operace add, sub_half, sub_full, inc, dec musí generovat OVER, pro případ, že jim programátor dal čísla se znaménkem.
Pro implementaci všech 4 "sčítacích" operací je potřeba použít pouze jedinou sčítačku. Protože ALU vždy vykonává pouze jednu vybranou operaci, jedna instance sčítačky stačí, a jednolivé operace se na ní musí "vystřídat".
Více informací v kapitolách o sčítání a odčítání.
Bonusové
Pro všechny bonusové operace platí, že můžete používat libovolné komponenty, kromě těch, které přímo implementují danou operaci.
Např. v mul můžete použít jakoukoliv sčítačku, ale ne (vestavěnou) násobičku. V cla nesmíte použít vestavěnout sčítačku. V barrel shifteru nesmíte použít jakýkoliv vestavěný shifter. etc.
| Typ | ID | Mnemo | Pseudokód | Popis |
|---|---|---|---|---|
| 🧑🎓 | mul16 | A MUL B | 16bit násobení A a B | |
| 🧑🎓 ❓ | mul8 | AL MUL BL | 8bit násobení spodních polovin A a B | |
| ❗ ❓ | swap8 | SWAP8 A | Výměna horního a spodního bytu A | |
| 🧑🎓 | mul16k | A MUL B | viz mul16 | 16b násobení pomocí Karatsubova alg. |
| 🧑🎓 | cla | A ADD B | viz add | Použijte místo add pokudjste implementovali CLA. |
| 🧑🎓 | bsh | A SHC B | Posun A o B doleva/doprava | |
| 🧑🎓 ❓ | bshl | A SHL B | Posun A o B doleva | |
| 🧑🎓 ❓ | bshr | A SHR B | Posun A o B doprava | |
| 🧑🎓 | bcd | BCD A | - | převod A na BCD |
Násobení (~2b)
Stačí implementovat násobičku kladných čísel podle naivního násobení pod sebou. Za pokročilejší řešení (násobení čísel ve dvojkovém doplňku, efektivnější násobička jako Dadda nebo Wallace multiplier) získáte větší počet bodů (indikujte v README).
Pro splnění násobení je potřeba implementovat buď mul16 (velká operace), nebo mul8+swap8 (menší operace + pomocná operace).
V obou případech bude možné násobit libovolně velké čísla v softwaru pomocí částečných násobků.
Doporučuji variantu mul8+swap8, protože bude v obvodu mnohem méně hradel, což urychlí simulaci.
V případě implementace barrel shifteru lze operaci swap8 vynechat, protože jí lze nahradit pomocí série operací bshl, bshr, or.
Alternativně lze za více bodů rozšířit mul8 na mul16 pomocí Karatsubova algoritmu (viz níže).
Karatsubovo efektivní násobení (~1b navíc k násobení)
Alternativní způsob implementace 16bit násobení, pokud už máte postavenou 8bit násobičku.
Standardně je pro implementaci 16bit násobení potřeba provést čtyři 8bit násobky (AL*BL, AL*BH, AH*BL, AH*BH) a posčítat správně výsledky. To odpovídá klasickému "naivnímu" školnímu násobení pod sebou.
Ovšem Anatolij Alexejevič Karacuba (anglicky Karatsuba) v roce 1962 publikoval algoritmus, pomocí kterého lze 16bit násobení provést pouze pomocí tří 8bit násobků, za cenu několika sčítání navíc.
Tento Karatsubův algoritmus se hodí primárně pro urychlení velkých násobků v softwarových rutinách, kde máme od hardwaru k dispozici pouze 8b/16/32b násobení. Počet hardwarových násobení, které je potřeba provést pro vypočtení nbit x nbit násobku je , což je podstatný rozdíl oproti naivnímu násobení pod sebou, kde je to .
Pro implementaci v HW se hodí spíše násobičky založené na efektivnější redukci součtů (Dadda, Wallace), nicméně pro porozumění algoritmu poslouží i jeho implementace v HW.
Buď:
- implementujte 8bit násbičku klasicky, nebo
- implementujte 4bit násobičku klasicky, a pomocí tří jejich instancí dle Karatsubova algoritmu zapojte 8bit násobičku.
Poté, pomocí tří 8bit násobiček dle Karatsubova algoritmu zapojte 16bit násobičku. Touto násobičkou implementujte operaci mul16, ale označte ji v OPCODES.txt jako mul16k.
Sčítačka s predikcí přenosů (CLA) (~2b)
Neboli Carry Lookahead Adder (CLA). Klasický postup sčítání zprava doleva (Ripple-carry adder) je pomalý. Analýzou vztahu carry-in jednotlivých full-adderů ke vstupům lze zjistit, že každý carry-in/out lze předpovědět přímo ze předchozích vstupů vypočtením několika násobků, které se sečtou. Tedy čas pro výpočet bude vždy pouze daný pouze rychlostí vícevstupového AND (kterých se provede několik paralelně) a následného vícevstupového OR. Při implementaci v tranzistorech je vícevstupový AND/OR rychlejší, než řetězec hradel XOR+OR, který najdeme v klasickém ripple-carry adderu (RCA).
Získáváme tedy recept na to, jak postavit sčítačku, kde rychlost výpočtu výsledku je kvazi-konstantní vůči šířce sčítačky, ovšem za cenu velkého nárůstu hradel (pro každý full-adder musíme přidat několik širokých AND a jeden široký OR). Velikost prediktoru roste s tím, jak daleko dopředu predikci provádíme. Má tedy smysl udělat určitý trade-off, a predikci někde uříznout. Např. postavit 4b adder s predikcí (velmi rychlý), a ten 4x zřetězit na 16b adder.
Více informací na wikipedii: Carry lookahead adder
Ovšem i po zřetězení 4x 4bit-CLA za sebe není potřeba čekat na ripple-carry propagaci zkrz tyto CLA. Lze použít stejný princip jako předtím, a každý ze čtyř COUT předpovědět ze vstupů ( a každého CLA lze vypočítat z a full-adderů uvnitř). Jednotce, která toto zaopatřuje se říká Lookahead carry unit (LCU), a je to dobře studovaný obvod.
Více informací na wikipedii: Lookahead carry unit
- 4bit-CLA, 4x zřetězeno - 1b
- 8bit-CLA, 2x zřetězeno - 2b (relativně velký obvod)
- 4bit-CLA + LCU - 2b
- jiná varianta - dle domluvy
Modifikujte svojí existující sčítačku, nevkládejte do ALU další. V OPCODES.txt indikujte místo add operaci cla.
Do full-adderu přidejte výstupy , . Pro přehlednost umístěte prediktor do samostatného modulu, který bude brát na vstupu všechny , , a CIN a na výstupu n-bitový COUT (nebo n-krát ).
V prediktoru se nesmí vyskytovat řetězec z CIN na nejvyšší COUT, to by mělo stejnou rychlost jako RCA. Je potřeba výraz pro predikci každého bitu plně vyexpandovat a vyjádřit jako součet násobků / sum of products (SOP) / disjunktivní normální formu (DNF), a zapojit pomocí vícevstupových hradel.
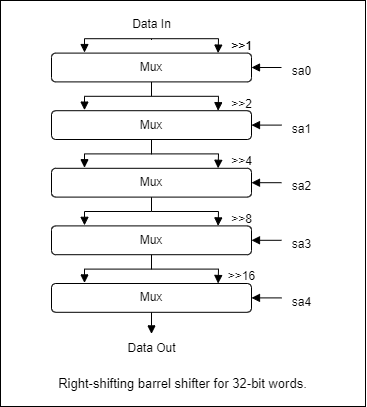
Logický posun A doprava/doleva o B míst (Barrel shifter) (~2b)
Pro implementaci posunu o libovolný počet míst se nabízí několik variant, nejefektivnější z hlediska využití tranzistorů je tzv. cross-bar shifter. Nicméně používá třetí stav (controlled buffery nebo na úrovni tranzistorů transmission gates), a proto není vhodný pro implementaci na FPGA, které třetí stav nepodporují.
Princip spočívá v rozložení velikosti posunu na součet mocnin dvou (to je jeho binární reprezentace, tu už máme!), a postupného provedení posunu o každou složku součtu zvlášť. Např. posun o 10 provedeme posunem o 8 a o 2 (posun o 4 a o 1 neprovedeme). Provedení/neprovedení posunu se dá přepínat multiplexorem.
Přehledný diagram implementace tohoto postupu se poměrně špatně hledá, proto ho uvádím zde:
Barrel Shifter pomocí multiplexorů (zdroj)
Barrel Shifter pomocí multiplexorů (zdroj)
Pro plný počet bodů je potřeba implementovat shift doleva i doprava, v jedné ze dvou variant:
bsh- posun doleva pokud , jinak posun dopravabshl+bshr- posun každým směrem jako zvlášť operace ALU (vhodné pokud vám zbývá dost volných hodnot selectoru)
Není potřeba řešit CIN a COUT jako u shl/shr.
Posun u 16bit hodnot dává smysl provádět o 0-15 míst, posun o více má za výsledek vždy 0. Vaše operace nemusí správně řešit větší hodnoty posunu než 15, stačí tedy brát v potaz pouze spodní 4 bity B.
Konverze z binárky na BCD (~2b)
Implementujte v ALU modul, který převede hodnoty 0-9999 na vstupu A na čtyřmístnou reprezentaci čísla v Binary Coded Decimal (BCD). Tato reprezentace je vhodná pro e.g. zobrazování hodnot v desítkové soustavě na 7-segmentovém displeji. Toto zobrazování budete mít následně jednodušší implementovat jako output v CPU, címž si zajistíte nějaké body za CPU IO.
Tedy bude obsahovat jednotky, desítky, stovky a tisíce hodnoty na vstupu interpretované v desítkové soustavě. Čísla na vstupu větší než 9999 nemusíte řešit. Takové čísla se vejdou do 14 bitů, takže stačí pracovat s těmito spodními bity vstupu.
Algoritmus, kterým se tento převod dá efektivně (bez dělení a modula!) provést, se jmenuje Double-Dabble. Dá se implementovat jak v SW (opakovanou aplikací porovnání a přičtení), tak v HW (zařazením za sebe tolik modulů provádějících porovnání+přičtení tak, aby se každému bitu stalo to samé, co v SW rutině). Příklad implementace v HW (pro větší hodnoty než máte zadáno) je na konci článku o Double-Dabble.
"Double" v algoritmu je pouze logický posun doleva, ten lze realizovat jednoduše úpravou zapojení vodičů do další fáze (je zdarma).
V jádrové operaci algoritmu "porovnání a podmíněné přičtení" se porovnává s konstantou (>4), a přičítá konstanta (+3). Obvody pro provedení těchto operací jdou oproti obecnému porovnání a sčítání dramaticky zjednodušit:
- Buď, jako jsme delali při úpravě výrazů v Booleově algebře (konstantní jedničky a nuly ve výrazu vždy lze nějak zjednodušit) - rozkreslit si 4b komparátor a 4b sčítačku s těmito konstantami na vstupu a zjednodušovat pomocí booleovy algebry (zapisovat hodnoty konstantních vodičů a škrtat nepotřebná hradla). Samotné rozhodnutí lze vyřešit malým multiplexorem.
- Přistupovat k modulu jako funkci o 4 vstupech a 4 výstupech, jejíž pravdivostní tabulku známe, testy sestavit vzorce pro každý z výstupů lze jednoduše pomocí Karnaughovy mapy.
Pouze řešení s efektivním komparátorem a zvětšovačkou bude hodnoceno plným počtem bodů.
Paměti - Sekvenční obvody
Kombinační obvody
Kombinační obvody lze ekvivalentně zadefinovat několika způsoby:
- Hodnoty výstupů jsou plně definované pouze hodnotami vstupů
- Obvod implementuje matematickou funkci, tj. lze popsat pravdivostní tabulkou
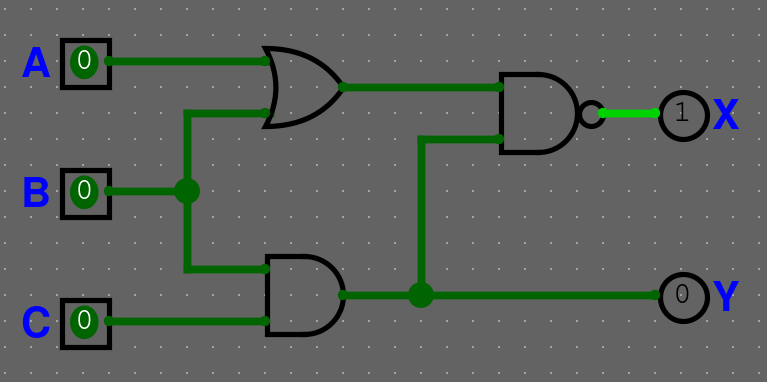
- V obvodu se nevyskytují žádné cykly (nepřímá závislost vstupu hradla na jeho výstupu)
Příklad kombinačního obvodu
Sekvenční obvody
Sekvenční obvody jsou ty obvody, které nejsou kombinační, tj. vyskytují se v nich nějaké cykly. Tyto cykly způsobují zajímavé chování (paměť), ale jsou obtížnější analyzovat.
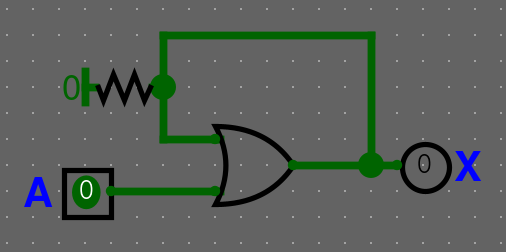
Příkladný sekvenční obvod s OR
Znázornění v pravdivostní tabulce
Protože X je zároveň výstup a vstup do obvodu, musíme tyto dvě jeho funkce rozdělit:
- - aktuální hodnota vodiče X, tj. vstup
- - příští hodnota vodiče X, tj. výstup.
"Příští" tady znamená, jakmile dané hradlo zpracuje své vstupy a aktualizuje svůj výstup - jeho tzv. propagační delay, který je vždy nenulový, závislý na výrobním procesu (typická hodnota např. 10ns). Tedy je to hodnota X v budoucnosti.
Nyní v pravdivostní tabulce můžeme popsat, jaké bude příští X v závislosti na aktuálním X a vstupu :
| A | X | X' |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Z chování obvodu vidíme, že pokud je , se nezmění (), a pokud , pak na nezáleží a . Můžeme tedy pravdivostní tabulku zjednodušit zavedením neznámé :
| A | X | X' |
|---|---|---|
| 0 | S | S |
| 1 | S | 1 |
V této tabulce může S nabýt libovolných hodnot ( nebo ) a každá varianta reprezentuje jeden řádek. Nicméně z takto zjednodušené tabulky je lépe vidět časové chování obvodu:
Pokud se obvod nachází v nějakém "stavu" , tak při v něm zůstane, ale při přejde do stavu .
Zároveň platí, že abychom mohli znát hodnotu výstupu, musíme znát hodnotu aktuálního stavu , který může být skrytý uvnitř obvodu, nestačí nám pouze vstup - typická vlastnost sekvenčních obvodů.
Popis výrazem a nekonečné vyhodnocování
Obvod můžeme popsat i výrazem:
kde značí příští hodnotu a tu stávající. Pokud nám ale vyjde jiné , než jsme měli , obvod na něj okamžitě zareaguje (je to vstup) a spustí výpočet znovu po dosazení za , tedy potenciálně je nutné popsat obvod takto:
Zde vidíme, že výraz se po opakovaném (klidně i nekonečném) dosazování za nemění. Z toho lze odvodit, že je garantovaně stabilní. Nemusí tomu tak být vždy
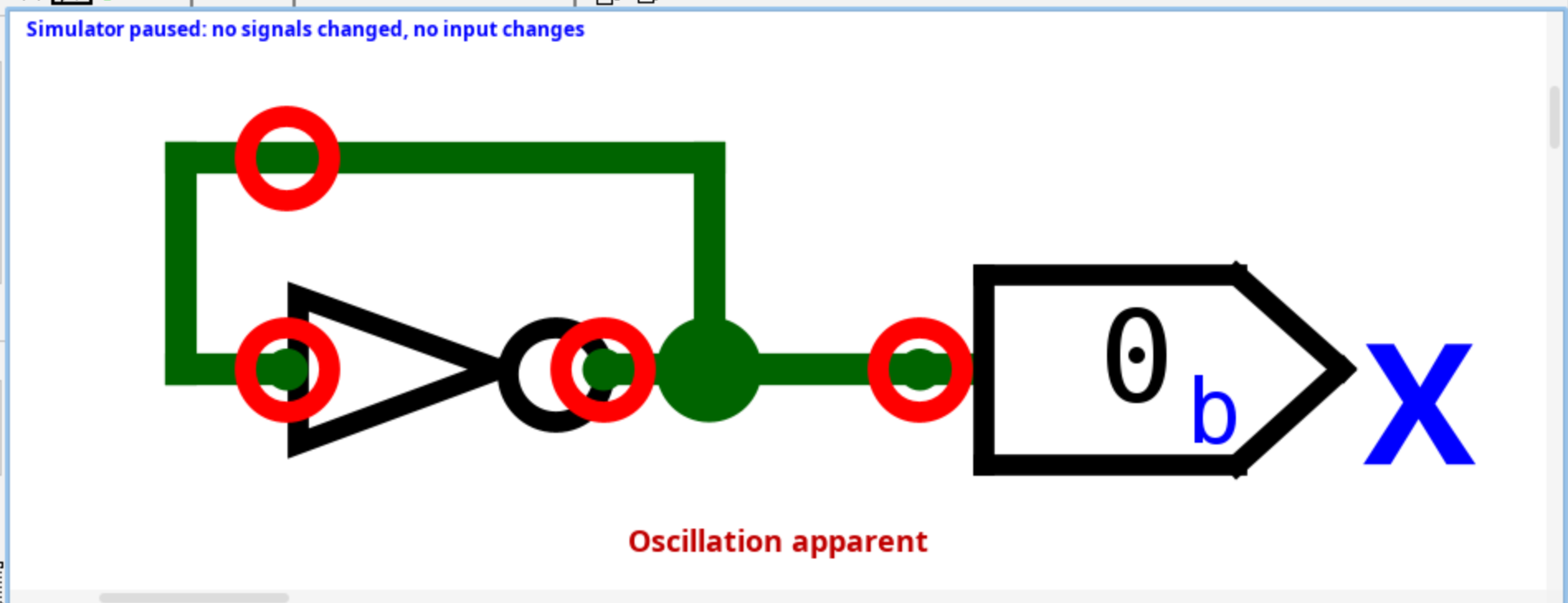
Nestabilní obvody
Nejjednodušší nestabilní obvod je následující obvod o nula vstupech:
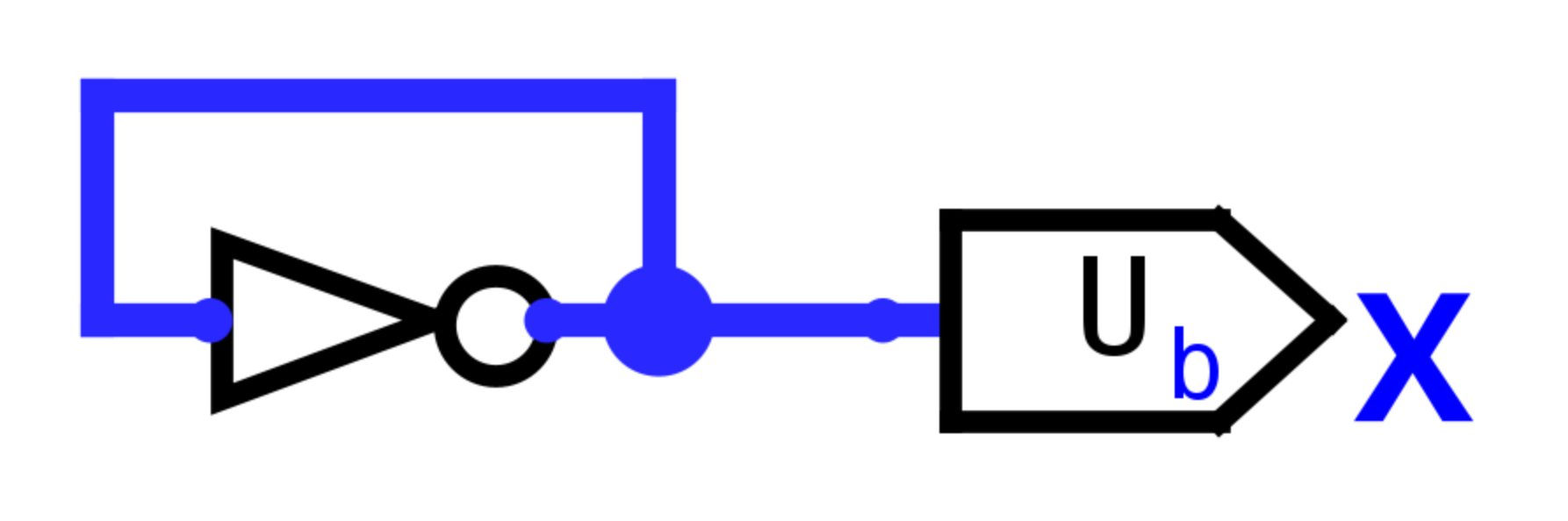
Tento obvod můžeme zase modelovat pomocí výrazu:
Pokud ale budeme opakovaně dosazovat, nedostaneme ten samý výraz. Označme (neznámý) počáteční stav , a stav po dosazeních (neboli po provedeních obvodu). Každý stav se vypočítává z toho předchozího.
Můžeme tedy říct, že protože a obecně , stav obvodu se po každém provedení hradla změní, a tedy není stabilní, nikdy se neustálí na jednu stálou hodnotu, neboli osciluje. Skutečně, potvrdí nám to i simulace Logisimem:
SR Latch
Sekvenční obvody můžete využít pro paměť pomocí hradla OR. Hradlo OR nám vstup zapne a nechá výstup neustále zapnutý, ale nemáme ho zatím jak vyresetovat.

Abychom ho mohli vyresetovat, přidáme další vstup a to R jako reset.
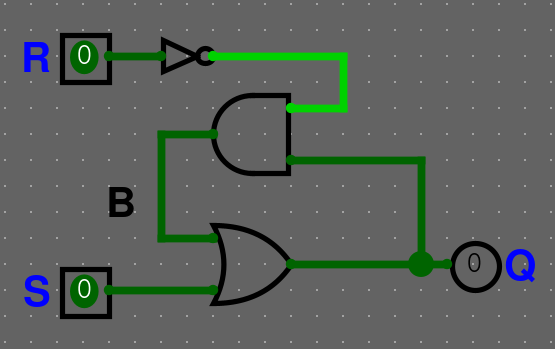
Zapíšeme do výrazu
Zapíšeme chování do pravdivostní tabulky
| R | S | Q | Q' |
|---|---|---|---|
| 0 | 0 | Q | Q |
| 0 | 1 | X | 1 |
| 1 | 0 | X | 0 |
| 1 | 1 | X | 1 |
Vytvořili jsme SR Latch, který se ale dá optimalizovat, tak abychom potřebovali 2 stejné gaty a to NOR viz. gif.
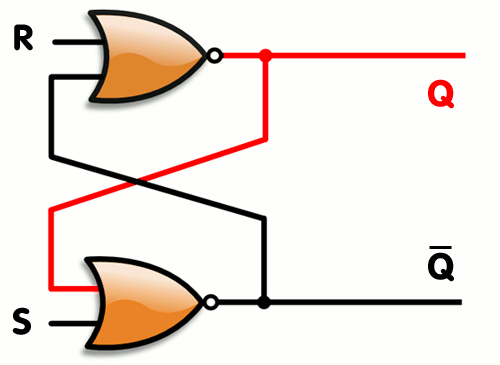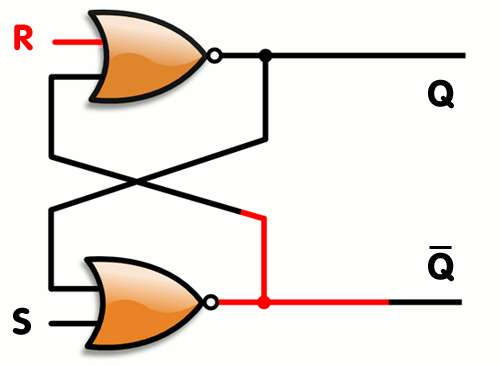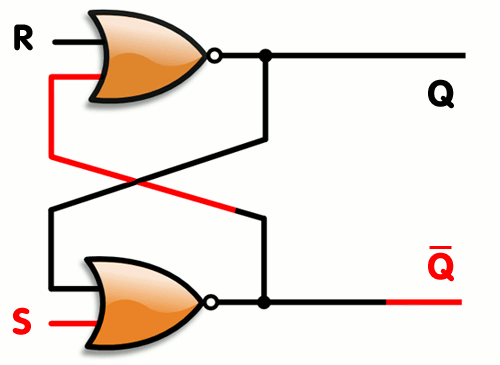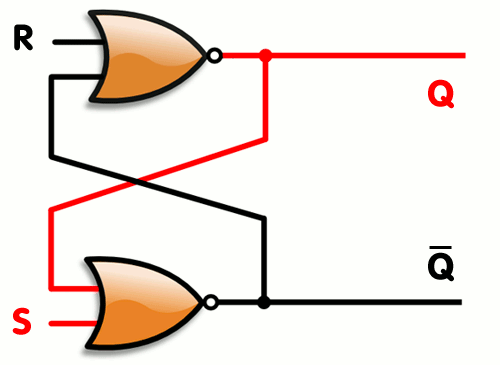
Latch vs Flip Flop
Signály
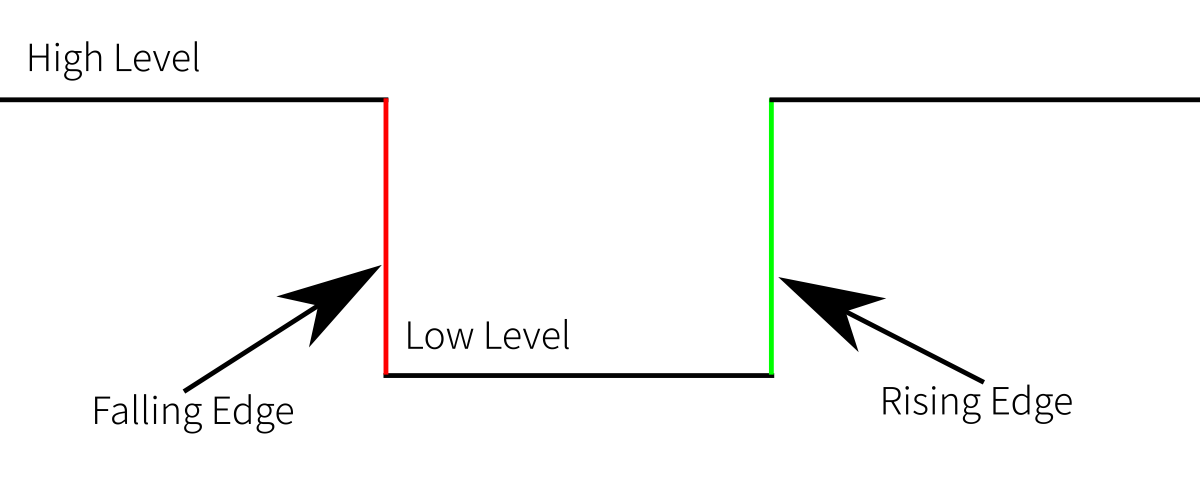
Na následujícím obrázku vidíme 4 definice.
High Level(Active-High) - zde probíhá ukládáníLow Level(Active-Low) - značí se jakoCLKneboENARising/Falling edgehodnota se zpracuje v okamžiku přechoduCLKsignálu z high na low a opačně
Latch
Latch je level-triggered. To znamená, že latch bere vstup, když je zapnutý viz. obrázek
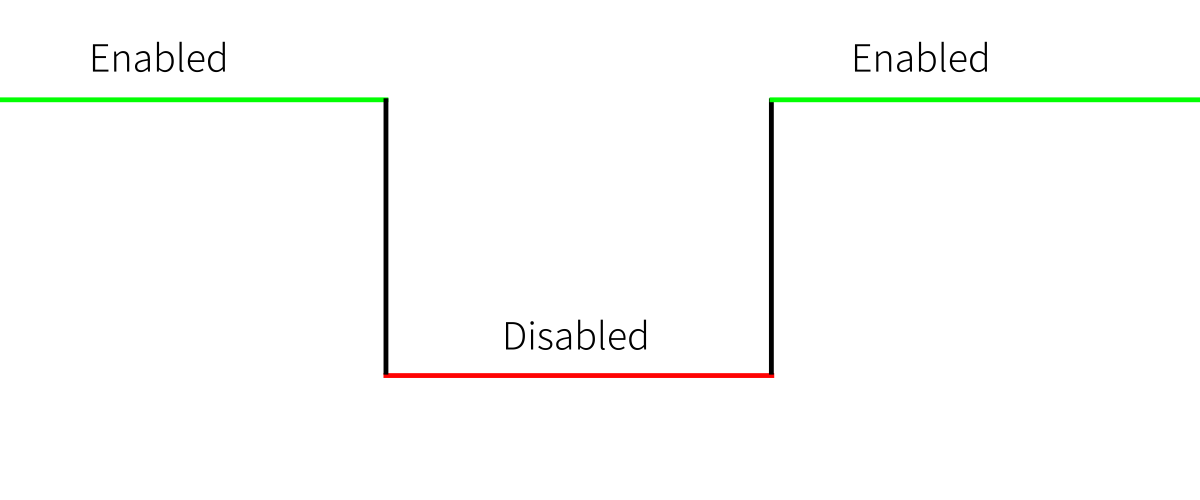
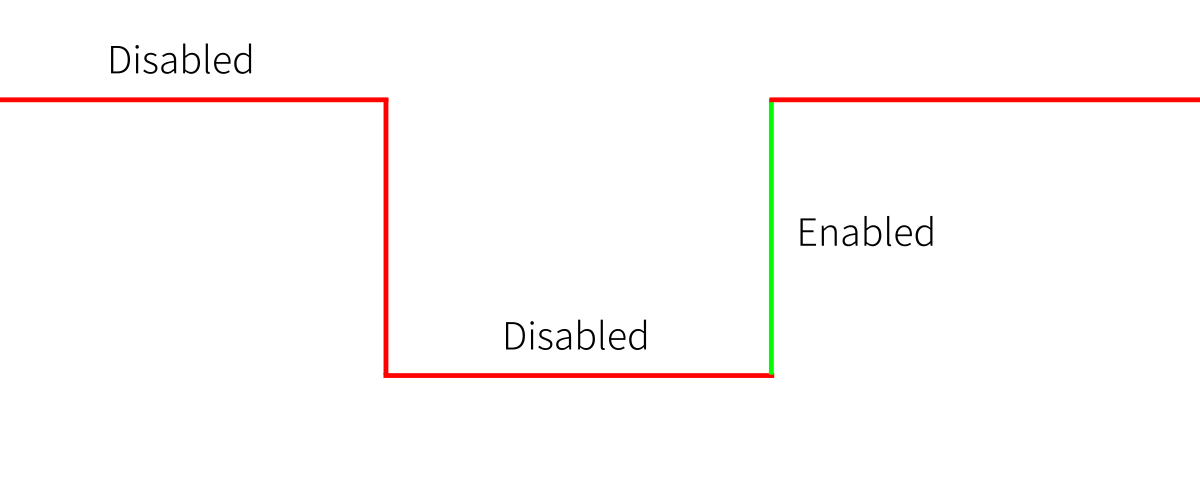
Flip Flop
Flip flop je edge-triggered. To znamená, že buď bere vstup na rising edge nebo falling edge. Na následujícím obrázku bere vstup na rising edge.
Oscillation apparent
V rámci sekvenčních obvodů můžete narazit na chybu Oscillation apparent. Znamená to, že jste v nějakém paradoxním cyklu. Vyřešíte to následovně:
- Odstraníme problémový prvek
Reset Simulation(CTRL+R)- Pokud není zapnuté tak -->
Auto-Propagate(CTRL+E)
Bonusové materiály
- Latch vs Flip Flop - https://www.youtube.com/watch?v=LTtuYeSmJ2g
- Latch a Flip Flop na wikipedii
- Anglicky (víc informací) - https://en.wikipedia.org/wiki/Flip-flop_(electronics)
- Česky - https://cs.wikipedia.org/wiki/Bistabiln%C3%AD_klopn%C3%BD_obvod
Paměti - Asynchronní obvody
Asynchronní obvody fungují bez clocku, takže jakmile je na vstupu hodnota, zpracuje se.
SR (Set-Reset) latch
SR latch jde vytvořit mnoho způsoby, nejčastější jsou SR NOR latch a SR NAND latch
Obrázek SR NOR latch
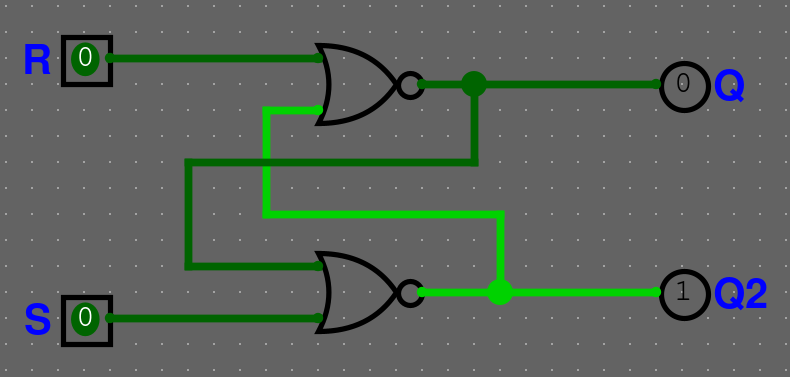
Obrázek SR NAND latch
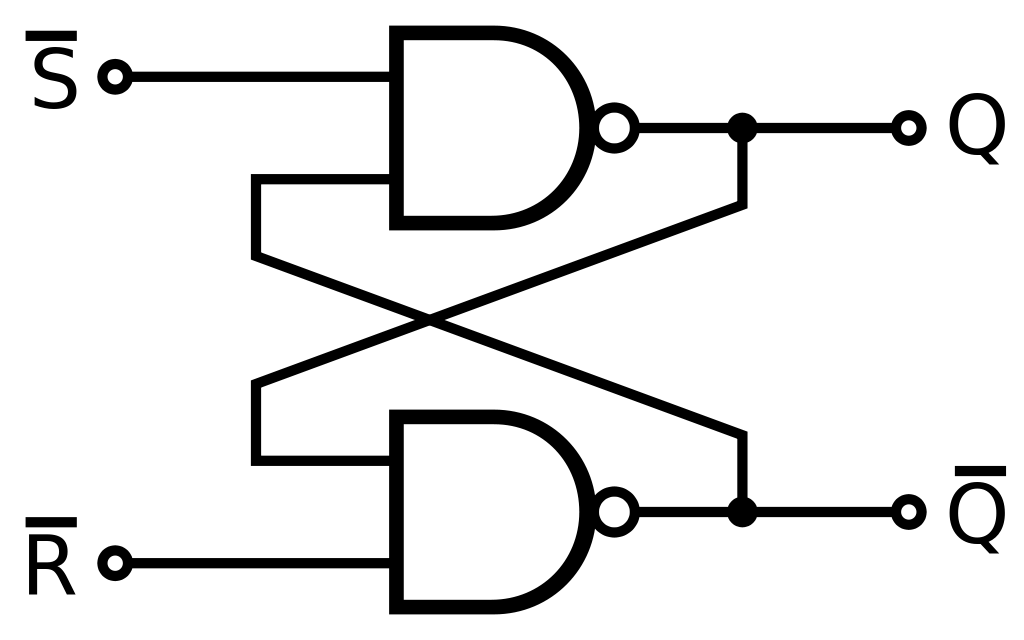
Pravdivostní tabulka
| S | R | Q' | Poznámka |
|---|---|---|---|
| 0 | 0 | Q | Beze změny |
| 0 | 1 | 0 | Reset |
| 1 | 0 | 1 | Set |
| 1 | 1 | ? | Set+Reset |
Jaké jsou rozdíly mezi SR NAND a SR NOR? (3)
Jaké jsou rozdíly mezi SR NAND a SR NOR? (3)
- Výstup při set+reset je u NAND 1, u NOR 0
- Vstupy set a reset mají u NAND invertovanou logiku
- U NAND SR je kladný výstup u hradla se set vstupem, u NOR SR je to opačně
JK latch
JK latch se primárně používá na toggle.
Pravdivostní tabulka JK latch
| J | K | Q' | Poznámka |
|---|---|---|---|
| 0 | 0 | Q | Beze změny |
| 0 | 1 | 0 | Reset |
| 1 | 0 | 1 | Set |
| 1 | 1 | Q | Toggle |
Gated D (data) latch
- Gatování - možnost vypnout či zapnout prvek, pomocí vstupu (typicky
ENABLE).
D latch využívá vstup enable jako 2 vstup. Tvořící sérii pravidel.
| E | D | Poznámka | ||
|---|---|---|---|---|
| 0 | - | Q | Beze změny | |
| 1 | 0 | 0 | 1 | Zápis 0 (reset) |
| 1 | 1 | 1 | 0 | Zápis 1 (set) |
Paměti - Synchronní obvody
Původní verze lekce viz asynchronní obvody
Synchronní obvody
Jsou ovládané extra clockem (CLK), který určuje kdy obvod pracuje. Příkladné obvody jsou:
- SR-flip-flop
- T-flip-flop
- D-flip-flop
V následující kapitole se podíváme na D-flip-flop, jelikož je nejzajímavější.
Jak synchronizovat obvod? (Rising/Falling edge detektor)
Vytvoření Rising/Falling edge detektoru viz. obrázek
Rising edge detektor (pomocí NOT delaye)
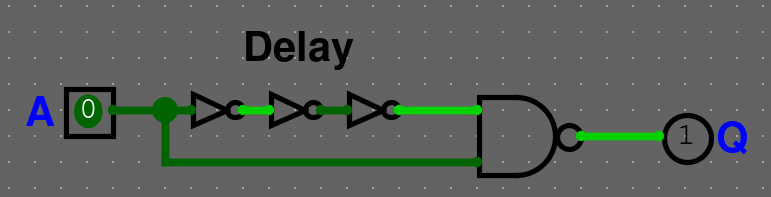
U falling edge detektoru jen prohodíme NAND gatu za AND gatu.
D (Data) Flip Flop
Pravdivostní tabulka
| Clock | D | |
|---|---|---|
Rising edge | 0 | 0 |
Rising edge | 1 | 1 |
Non-rising | X | Q |
D flip-flop jde vytvořit mnoha způsoby. Ukážeme si dva, a to klasickou variantu a master-slave variantu.
Master-slave D-flipflop
Vytvoříme ho pomocí 2 Gated D-latch. Pozor, aktivuje se na Falling edge.
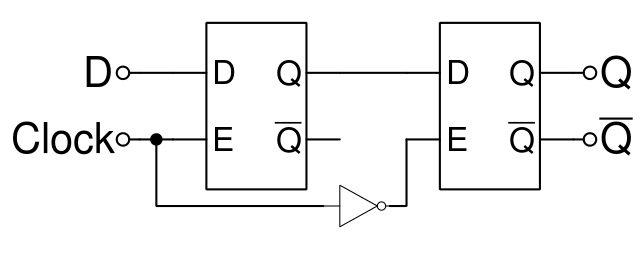
Varianta pro Rising edge.

Optimalizovaná varianta
Můžeme vystavět pomocí 6 NAND gate.
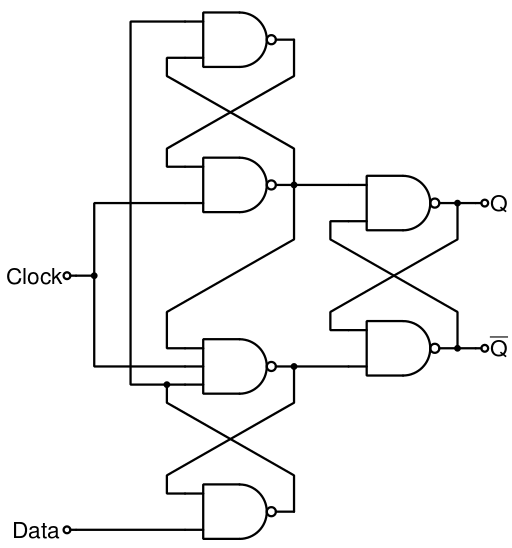
Můžeme přidat 2 vstupy pro asynchronní set a reset. Stačí jenom NAND gaty vyměnit za 3-vstupové.
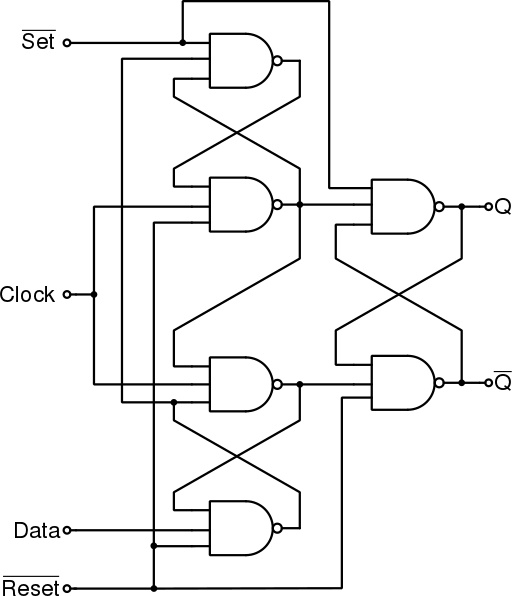
Registr
Pokud chceme ukládat vícebitové hodnoty, stačí položit několik D-flip-flopů vedle sebe:
Shift Register
Shift register je užitečná varianta registru. Je tvořen z několika D flip-flopů zapojených v zřetězení do sebe. Při každém clocku se hodnoty v shift registru posunou o jednu pozici po směru toku dat. To umožňuje shift registr naplnit v čase za sebou přicházejícími 1bit hodnotami a následně pracovat s celou hodnotou.
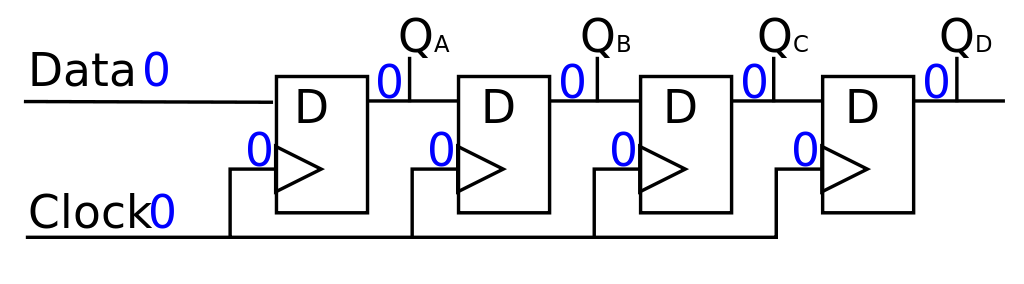
Bonusové materiály
- Shift register anglická wikipedie - https://en.wikipedia.org/wiki/Shift_register
- Flip-flopy a latche - https://en.wikipedia.org/wiki/Flip-flop_(electronics)
Návrh sekvenčních obvodů
Rozhraní typického sekvenčního obvodu
Vstupy a výstupy
Typický plně synchronní sekvenční obvod bude mít kromě datových vstupů a výstupů navíc následující vstupy a výstupy, které řídí sekvenční povahu obvodu:
CLK- vstup hodinového signálu. Hodinové vstupy všech obvodů v jednom sekvenčním obvodu musí být vždy propojené, aby obvod představoval jedinou hodinovou doménu. V opačném případě se vystavujeme nebezpečí.START- pokud je vstupSTART=1, inicializuj výpočet podle aktuální hodnoty vstupů, nehledě na to, zda aktuálně nějaký výpočet probíhá. Rovněž je možné (jako optimalizace) během toho cyklu provést první operaci výpočtu, ale není to nutné. Až přiSTART=0je možné ve výpočtu pokračovat, a časem ho dokončit.DONE- pokud je na výstupuDONE=1, je výpočet hotový, a výsledek na datových výstupech je validní. Jakmile tohle nastane, musí obvod držet výstupy v neměnném stavu a dále držetDONE=1, až do příštíhoSTART=1. V momentě, kdy se zpracujeSTART=1, musí být na výstupuDONE=0(obvod se inicializoval pro další výpočet => výpočet není hotový), aby mohl vnější uživatel očekávatDONE=1. Vyjímečně, pokud je výpočet hotový hned v inicializačním cyklu (např. násobička identifikovala násobení nulou => výsledek je triviálně nula), může ihned indikovatDONE=1.
Synchronizace s hodinovým vstupem
Synchronní obvod může být synchronizovaný buď na sestupnou nebo na náběžnou hranu hodin, nebo využívat obě hrany (tato technika se nazývá Double Data Rate, neboli DDR, což znáte z počítačových pamětí). Návrh používající DDR je vhodný pouze pro realizaci v silikonu (ASIC), nikoliv pro FPGA, kde paměťové prvky reagují buď na jeden nebo druhý typ hrany.
Sekvenční algoritmy probírané na hodinách
Všechny Logisim soubory z hodin jsou ke stažení zde.
Naivní násobení pomocí iterovaného sčítání
Princip: Pro výpočet provedeme -krát . Pokud začínalo na , tak po těchto iteracích bude .
Tento algoritmus je neskutečně neefektivní, protože počet provedených operací stoupá lineárně s hodnotou B (složitost ). Typicky se snažíme, aby počet operací byl úměrný počtu bitů B, tedy aby složitost algoritmu byla . Takovou složitost má právě metoda double-and-add popsaná dále.
Násobení pomocí metody Double-And-Add
Pro urychlení násobení lze využít tzv. Hornerovo schéma pro násobení polynomů:
Neboli začínáme s hodnotou 0 (neutrální prvek vůči sčítání), a v každém cyklu zpracujeme jeden bit hodnoty B od MSB: pokaždé hodnotu výnásobíme 2, a pak přičteme buď nebo , právě podle hodnoty bitu z . Proto se algoritmus jmenuje Double-And-Add.
Při zapojení lze provést optimalizaci, kde přeskočíme první iteraci Double-And-Add, protože její výsledek je triviální: Pokud , pak výsledek iterace je , jinak je .
Umocňování pomocí metody Square-And-Multiply
Stejný princip lze použít i pro umocňování, pouze s vyššími operátory: Začínáme s hodnotou 1 (neutrální prvek vůči násobení), a v každém cyklu umocníme na druhou, a pak podmíněně vynásobíme hodnotu podle bitu z :
Více informací o tomto algoritmu je k dispozici v KBB přednášce, kde se používá pro modulární umocňování, a taky v KBB skriptech.
Double-Dabble algoritmus
Popis algoritmu viz zadání ALU. Principem sekvenčního provedení je skutečnost, že pokud explicitně provedeme posun, provádí se jádrová operace algoritmu vždy na ty samé bity. Zároveň lze provést vždy až 4 operace paralelně, jednu na každém řádu (jednotky, desítky, etc.). Modelujeme tedy softwarovou variantu algoritmu, ale opravování číslic provádíme vždy 4-paralelně.
Příklad plného zadání: Umocňování pomocí metody Square and Multiply
Specifikace modulu
Postavte plně sekvenční modul synchronizovaný na nábežnou hranu, který realizuje umocnění 4-bitového základu (vstup A) na 3-bitový exponent (vstup B), tedy spočítat operaci , během jednoho načítacího a 3 výpočetních cyklů (tedy dohromady během 4 cyklů). Výstup musí být alespoň 28-bitový, aby se do něj vešel maxímální možný výsledek (). Pro jednoduchost řekněme, že výsledek bude 32-bitový. Modul se bude jmenovat EXP a můžete (máte) v něm používat logisimové matematické operace, e.g. násobení. Pro implementaci stačí dvě násobičky, víc pro sekvenční implementací umocňování není potřeba.
Časování
Modul je plně synchronní, reaguje na vstup a mění svůj výstup tedy pouze s náběžnou hrannou vstupu clk.
Pokud je na vstupu start=1, načte modul vstupy a připraví se na výpočet (toto může nastat i během již probíhajícího předchozího výpočtu, v takovém případě se tento výpočet ruší a připraví se nový podle vstupů). "Příprava na výpočet" může znamenat různé věci: pouhé uložení vstupních hodnot do registrů, nebo přímo provedení prvního kroku výpočtu podle vstupů a uložení částečného výsledku do registrů. V každém případě by se ale měla inicializovat řídící část obvodu - pokud obvod provádí výpočet v nějakých "krocích", nebo má v registrech jiné poznámky o výpočtu, je potřeba tyto inicializovat na hodnoty, které umožní začít výpočet od začátku.
Jakmile start=0, provede modul s každým clockem jeden krok výpočtu. Během tohoto musí být výstup done=0. Modul může počítat s tím, že po celou dobu jednoho výpočtu zůstanou vstupy A a B konstatní. Jakmile modul dokončil výpočet a na výstupu OUTP prezentuje správný výsledek, musí přestat počítat (výsledek musí zůstat konstantní, dokud nepřijde další start=1 signál). Zároveň toto musí indikovat pomocí done=1.
Pamatujte, že synchronní obvod reaguje na hodnoty na vstupu až při příští náběžné hraně, ne té, která změnu hodnoty způsobila!
Příklad průběhu výpočtu modulu:
Popis událostí (ticků) v diagramu:
- 1: Uživatel zadefinoval A a B a zadal
start=1. Modul o tom ale zatím neví, na tuto změnu bude moct zareagovat až v přístím cyklu. - 2: Modul zpracoval
start=1: inicializoval interní registr (a tímpádem i OUTP) na 1, změnildone=1. - 3-4: Dva cykly výpočtu .
- 5-6: Modul reaguje (dvakrát za sebou) na inicializační požadavek
start=1od uživatele. Aktuálně probíhající výpočet se ruší bez výsledku a inicializuje se nový výpočet s novými vstupy. Druhý požadavek nemá na hodnoty (vnitřní i výstupy) už žádný další vliv, protože už mají správnou hodnotu. - 7-9: Tři výpočetní cykly . OUTP průběžně reflektuje částečný výsledek (ale toto chování není zdokumentované a uživatel by tuto hodnotu měl ignorovat!).
- 9: Posledním výpočetním cyklem se nastaví
done=1a na výstupu je správný výsledek. Ten tam vydrží, až do té doby, než se zpracuje přístístart=1(což je tady až ve 12. ticku).
Příklad řešení
Ke stažení zde.
Další zadání a informace k testu
Test
Test se sekvenčních obvodů proběhne prezenčně na hodině v online prostředí Logisim za následujících podmínek:
- Zadání testu bude přístupné v lokální (neveřejné) kopii skript, kterou můžete během testu používat
- V online Logisimu bude zapnutá simulace, analýza, etc - nic nebude omezeno
- Bude povoleno používat všechny Logisimové komponenty - hradla, plexery, aritmetiku, paměti
- s výjimkou těch, které přímo řeší zadání (e.g. násobička, pokud zadání je násobení)
- a těch, které jsou pro zadání nepřiměřeně komplexní (e.g. procesor, velké paměti RAM, etc.)
- počet některých komponent může být omezen, aby bylo nutné výpočet provádět sekvenčně (e.g. jedna sčítačka, pokud zadání je násobení nebo výpočet výrazu)
Obecné kompetence
Pro úspěch v testu, tj. prokázání schopnosti postavit funkční sekvenční obvod podle zadání, je potřeba ovládat následující věci:
- Registry s Write-Enable, jejich synchronní chování
- Multiplexory pro rozhodování mezi variantami na nějakém vodiči/vstupu podle kontrolního signálu
- Shift registry, pro paralelně-sériovou konverzi, zejména:
- zpracování sekvenčního vstupu (hodnoty příchází postupně ale jsou potřeba najednou)
- ukládání průběžných výsledků (které jsou dostupné postupně) pro paralelní odevzdání na výstup
- Rozvržení paměťové části obvodu - jaké registry budou potřeba pro e.g. mezivýpočty, co v nich kdy bude, jak velké budou
- Návrh datové cesty, tj. úvaha nad tím, jakými všemi způsoby musí být data schopna z registrů a vstupů téct obvodem (provést nějaký výpočet) a zpátky do nějakých registrů nebo výstupů.
- Realizace této datové cesty pomocí multiplexorů a kontrolních signálů, bez třetího stavu
- Zpracování problému v krocích, tedy:
- Návrh algoritmu na úrovní RTL (Register Transfer Level), tj. co-kudy-kam poteče v každém kroku.
- Převod popisu RTL na popis pomocí kontrolních signálů, tj. jaké kontrolní dráty musí mít jakou hodnotu, aby se stalo to, co popisuje RTL, v každém jednotlivém kroku.
- Zapojení kontrolní jednotky, tj. (pravděpodobně) stepperu a následného výpočtu kontrolních signálů z aktuálního kroku a případně z aktuálního stavu dat v registrech
- Návrh kombinačních obvodů, buď intuitivně nebo podle pravdivostní tabulky
- Je potřeba pro výpočet kontrolních signálů v kontrolní jednotce, případně pro návrh nějakého výpočtu v datové cestě
- Je zde možné využít pomocné nástroje a kalkulačky vestavěné v Logisimu.
Tyto kompetence odpovídají látce probírané na hodinách před testem.
Možné příklady zadání
Zadání, které dostanete, nebude přesně odpovídat žádnému z tady uvedených, ale potřebné kompetence a složitost jsou podobné. V opravdovém zadání se vyskytnou prvky z těchto zadání. Pokud všechny z těchto zadání zvládnete zapojit, nebudete mít s testem problém.
Světelný had
N-bitový výstup LIGHTS světelného hada je připojen k řadě N LED světel. Rozsvícená je vždy pouze jediná LED. Dokud je vstup WE=0, tato rozsvícená LED "cestuje" v řetězci LED světel nahoru (směrem k 15. bitu výstupu), a jakmile dorazí na konec, kde stráví přesně jeden cyklus hodin, začne zase cestovat dolů. Na spodním konci se zase otočí a cestuje nahoru, do nekonečna.
V případě, že WE=1, musí se na výstupu (až s další hranou clk, jedná se o sekvenční obvod!) rozvítit N-tá LED podle hodnoty N na vstupu POS (tedy zápis "adresy" hada zvenčí - proto se vstup jmenuje WE - Write Enable). Až jakmile při hraně clk není WE=1, je had "vypuštěn", udělá jeden pohyb a poté se pohybuje normálně dál. Vypuštěný had se vždy začne pohybovat prvně směrem nahoru, kromě případu, kdy POS bylo 15, v takovém případě had rovnou narazil a začíná se pohybovat dolů.
Před prvním zápisem (WE=1) je chování hada nedefinované a nebude testováno.
Možná varianta by např. měla dva nezávislé hady na jednom LED pásku, a jednobitový vstup navíc určující, kterého hada zapisujeme.
Posuv/Rotace o N
Modul implementuje sekvenční shift/rotaci doleva/doprava o SHIFT bitů. V každém cyklu provede posun o 1 bit, dokud nemá hodnotu posunutou o SHIFT bitů. Platí standardní interface (start+done).
Klouzavý součet/průměr N hodnot
Tento sekvenční modul je tzv. proudový, tzn. zpracovává proud (stream) dat. Modulu přichází na INP postupně za sebou hodnoty, a z posledních N hodnot je potřeba spočítat součet/průměr (pokud je N mocnina dvou, jsou tyto zadání v podstatě ekvivalentní a žádná dělička není potřeba!). Takovému součtu/průměru se říká "klouzavý".
Hodnotu na vstupu bereme v potaz (zahrneme jí do výpočtu) pouze, pokud WE=1. Tedy pokud WE=0, výsledek se nesmí změnit!. Hodnota výsledku je nedefinovaná (nebude testována), dokud modul nezpracoval alespoň N hodnot.
Nápověda: Evidentně bude potřeba nějak mít uložených vždy posledních N hodnot. Na to se hodí shift registr, buď manuálně postavený, nebo ten logisimový.
Proudový detektor vlastností posloupnosti
Jednobitová varianta:
Vícebitová varianta:
Obvod zpracovává hodnoty ze vstupního proudu bitů nebo hodnot (pokud WE=1, jinak vstupy ignoruje). V posledních N (konstanta) hodnotách se snaží najít nějaký vzor, posloupnost s určitými vlastnostmi, etc. Pokud takový vzor našel, indikuje MATCH=1. Pokud to dává smysl podle zadání, zároveň indikuje číslem na výstupu nalezenou vlastnost nebo její parametr, viz konkrétní zadání níže.
Takových detektorů bude typicky založen na shift registru/registrech, který používáme na uložení posledních N hodnot, nebo nějaké vlastnosti vypočítané z hodnoty nebo z posledních několika hodnot.
Příklady možných detektorů pro jednobitovou variantu:
- Detekuj pattern '10011' (bit úplně vlevo přišel jako poslední)
- Detekuj situaci, kde v posledních N bitech (sudé N) je stejný počet 0 a 1.
- Nápověda: Pro nízke N je možné sestavit pravdivostní tabulku detektoru této vlastnosti, a implementovat ho pomocí Karnaughovy mapy, nebo pomocí nástrojů vestavěných v Logisimu.
- Detekuj situaci, kde sekvence N bitů tvoří palindrom
- ...
Příklady možných detektorů pro vícebitovou variantu
- Detekuj situaci, že všech N posledních čísel bylo sudých
- Nápověda: Jak na čísle reprezentovaném v binárce poznáme, že je sudé? Je potřeba ukládat N samotných čísel, nebo nám stačí ukládat jejich sudost?
- Detekuj v posledních N číslech aritmetickou posloupnost, tj. že každé číslo je o libovolné K větší/menší než to předchozí. Koeficient K posloupnosti posíláme na výstup VALUE. Použij jednu odčítačku.
- Poznámka: Koeficient K může klidně být záporný (ve dvojkovém doplňku), tj. posloupnost je klesající. Na obvodu to nic nemění, záporné číslo je taky číslo.
- Nápověda: O aritmetickou posloupnost se jedná, pokud rozdíl sousedních čísel je nějaká jedna hodnota. Máme jedno odčítačku, takže nemůžeme rozdíly počítat paralelně, musíme je počítat hned, jak čísla přicházejí. Neukládáme tedy samotné přicházející čísla, ale pouze rozdíly mezi nimi. K tomu samozřejmě musíme uložit i jedno předchozí číslo, abychom měli proti čemu rozdíl počítat.
- Detekuj v posledních N číslech geometrickou posloupnost s daným předem určeným koeficientem K (pro koeficienty, které jsou mocnina dvou je možná optimalizovaná implementace, v ostatních případech je nutné použít násobičku).
- Poznámka: Oproti předchozímu příkladu je zde koeficient zafixovaný zadáním - umíme tedy detekovat pouze jeden konkrétní "typ" geometrické posloupnosti. Tím se vyhneme nutnosti dělit. Navíc, pokud je koeficient mocnina dvou, stává se násobení jím triviální, a není potřeba ani násobička. Pokud je koeficent mocnina dvou plus jedna nebo mínus jedna, stačí místo násobičky sčítačka.
- Nápověda: Potřebujeme ověřit, že v posloupnosti platí , tedy že každé přicházející číslo je -násobek předchozího. Ukládáme tedy předchozí přijaté číslo, a vynásobíme ho s . Pokud se příští přijate číslo rovná této hodnotě, tvoří poslední dvě přijaté čísla žádanou posloupnost. Tuto pravdivostní hodnotu uložíme do shift registru. Posloupnost délky jsme nalezli, pokud v tomto shift registru o délce jsou samé .
- ...
Proudový analyzátor vyváženosti
Analyzátor beží do nekonečna a na výstupu vždy indikuje vyváženost počtu 0 a 1 ve vstupním proudu od jeho inicializace, tedy nevíme předem z kolika bitů musíme tuto vlastnost vypočítat, není tedy možné ukládat samotné bity, musíme je zpracovávat průběžně.
Je potřeba držet si "vyváženost", tj. číslo se znaménkem ve dvojkovém doplňku, které značí, o kolik víc jedniček, než nul, jsme viděli. Tuto hodnotu dávame na výstup BALANCE. Alternativně lze separátně držet počet jedniček a počet nul a tu pak odečíst, výsledek bude stejný. Výstup BALANCED indikuje, že BALANCE je 0, tj. počet jedniček a nul byl stejný. Pro zobrazení hodnot ve dvojkovém doplňku během vývoje doporučuji Probe, nastavenou na Radix: Signed Decimal.
Protože modul musí začít ve "vyváženém" stavu, ale iniciální hodnota všech pameťových buňek je doopravdy náhodná, potřebuje tento modul navíc (také synchronní) vstup INIT, pomocí kterého lze modul přivést do dobře definovaného, iniciálního, "vyváženého" stavu. Co to konkrétně znamená, záleží na zvolené vnitřní reprezentaci dat v modulu.
Výpočet matematického výrazu / provedení algoritmu (!!!)
Varianta s paralelními vstupy:
Varianta se sériovým vstupem:
Modul musí vypočítat zadaný výraz (e.g. ) pomocí předem určené výpočetní jednotky/jednotek (e.g. jediné sčítačky). Modul musí tento výraz pomocí vhodného, vámi navrženého, algoritmu ve více krocích vypočítat, výsledek vystavit na výstup OUTP a indikovat DONE=1. Platí standardní interface start-done.
U paralelní varianty je buď garantované, že vstupy zůstanou po celou dobu jednoho výpočtu konstantní, anebo tomu tak není, a vstupy se mohou během výpočtu měnit, a jsou validní pouze v tom cyklu, ve kterém byl START=1. Hodnoty vstupů mimo tento moment nesmíme použít, nejsou to hodnoty pro nás! O kterou variantu se jedná bude upřesněno v zadání.
U sériové varianty typicky platí, že počínaje cyklem, kde START=1, bude v každém clocku na vstupu INP jedna z potřebných hodnot, v nějakém pořadí, e.g. A-B-C-D. Nemusí to ale být vždy přesně takto: první hodnota může být k dispozici např. až v následujícím cyklu po START=1. Na hodnotu je pak potřeba jeden cyklus počkat. Zároveň můžou mezi jednotlivými hodnotami být mezery - např. předchozí modul hodnoty vypočítává průbežně a nemá je k dispozici hned za sebou. Pokud v následující notaci číslo značí prodlevu tolika cyklů, ve kterých nejsou na vstupu žádné užitečné data, proud hodnot na vstupu může mít např. následující podobu: 1-A-2-B-2-C-D (první startovní cyklus, nedostáváme nic, potom A, potom dva cykly nic, potom B, ...). Hodnoty je pak potřeba ze vstupu přečíst ve správnou dobu. Během toho čekání je možné provádět nějaké výpočty, ale není to nutné, počet cyklů odevzdaného obvodu nemusí být optimální.
Ukázkové zapojení paralelní varianty pro výraz s postupem je k dispozici zde.
Další příklady výrazů k výpočtu:
- pomocí jediné sčítačky.
- Na výpočet stačí 4 cykly, plus případné registrování vstupů/výstupů.
- Nápověda: Násobení mocninou dvou lze provést posunem, který je instantní, a . Násobička tedy není potřeba.
- pomocí jediné násobičky a sčítačky
- Nabízí se dvě varianty implementace. Druhá varianta bude pomalejší a komplexnější.
- V každém cyklu vynásobit + možná sečíst
- V každém cyklu vynásobit anebo sečíst
- Nápověda: , tento výpočet je potřeba provést ve dvou cyklech.
- Nabízí se dvě varianty implementace. Druhá varianta bude pomalejší a komplexnější.
- , tedy faktoriál
- Výsledky budou velké, použijeme tedy 32-bitové čísla. I tak budeme schopni spočítat nejvýše , vstupní hodnota může tedy být 4 bitová.
- Nápověda: Bude potřeba udržovat si čítač, který projede rozsah od do včetně (nebo od do , což možná vyjde lépe) a výpočet provádět v akumulátoru, který začně neutrálním prvkem pro násobení.
- , kde , pomocí jedné sčítačky/odčítačky
- je v tomto případě další vstup, jako .
- Obecné modulo vyžaduje děličku, kterou nemáme k dispozici. Ovšem, protože všechna čísla na vstupu jsou menší než , jediné případy, kdy bychom se mohli dostat během výpočtu mimo rozsah hodnot modulární grupy, jsou následující:
- Pokud výsledek součtu má hodnotu , nebude ale určitě mít hodnotu , modulo tedy lze provést pomocí pouhého odečtení .
Matematicky: - Pokud výsledek odečtení má hodnotu , nebude ale určitě mít hodnotu , modulo lze tedy provést přičtením .
Matematicky:
- Pokud výsledek součtu má hodnotu , nebude ale určitě mít hodnotu , modulo tedy lze provést pomocí pouhého odečtení .
- Po každém příčtení/odečtení v průběhu výpočtu je tedy potřeba zkontrolovat, zda jsme se nedostali mimo rozsah hodnot příjatelných jako výsledek , a pokud ano, provést korekci přičtením/odečtením . Protože máme pouze jedinou sčítačku, musí se tato korekce stát až v následujícím cyklu.
- Algoritmus výpočtu může tedy vypadat nějak takto:
- Tento postup je příklad často používané techniky, kdy jsou požadavky na výsledek jendodušší zajišťovat průběžně jednoduchým výpočtem, místo komplexním výpočtem na konci. Příklad z praxe je např. výpočet kroku MixColumns v šifře AES - zde se násobí polynom polynomem modulo polynom z . Spočítat polynomiální modulo je náročné, ale pokud postupujeme při násobení bit po bitu, můžeme místo závěrečného modula průbežně aplikovat podmíněný xor: "If processed bit by bit, then, after shifting, a conditional XOR with should be performed if the shifted value is larger than (overflow must be corrected by subtraction of generating polynomial)."
Je možná varianta tohoto zadání, kde místo matematického výrazu (který je potřeba prvně převést na algoritmus), bude poskutnut přímo algoritmus k implementaci.
Dalšími příklady jsou algoritmy probírané na hodinách, ke kterým je k dispozici i implementace v Logisimu.
Logisim soubory z hodin
- sekv_exp_sq_mul.circ 📎
- Umocňování Sq-Mul pomocí kombinačního square a kombinačního multiply (dvě násobičky, 4 cykly)
- Umocňování Sq-Mul pomocí jediné kombinační násobičky (6 cyklů, ale poloviční kritická cesta = dvojnásobná maximální frekvence!)
- 32bit Násobení Double-Add (jedna 32bit sčítačka, 33 cyklů)
- Umocňování Sq-Mul pomocí sekvenční násobičky Double-Add (až 171 cyklů, ale pomocí jediné 32bit sčítačky - obrovská maximální frekvence)
- sekv_double_dabble.circ 📎
- Algoritmus Double-Dabble na převod do BCD (bonusová operace ALU)
- 17 cyklů, ale pouze 4 instance jádrové operace algoritmu
- sekv_compute_expr.circ 📎
- Výpočet výrazu pomocí jediné sčítačky
CPU - Úvod
CPU neboli Central Processing Unit je užitečný pro jakýkoliv logický problém. Zvládne využívat tupé jednotky vašeho počítače a rozhoduje, co mají dělat...
Legenda k obrázku:
- červená - control flow
- černá - data flow
CPU se typicky skládá z:
- Control Unit (CU) - rozřazuje instrukce
- Registry - často velmi rychlé paměti CPU
- Kombinační logika - obecné kombinační obvody, zde patří například vaše ALU
- Main Memory - typicky RAM nebo ROM
- Input/Output - vstupy výstupy vašeho CPU
Sběrnice (bus)
Sběrnice typicky přenáší informace mezi komponenty ve vašem CPU. Nejlíp se to vysvětlí na datové sběrnici, která přenáší různá data mezi registry, output z ALU apod.
Typicky během instrukce pošlete nějakou hodnotu na sběrnici. Takže například chcete přesunout hodnotu registru B do registru C, tak vyšlete hodnotu registru B na sběrnici (enable) a nastavíte hodnotu registru C na hodnotu sběrnice (set).
Typy:
- adresová/address - typicky pro adresy v paměti
- datová/data - pro vysílaná data
- řídící/control - kominukaci mezi komponenty
CPU - Návrh
Průvodce návrhem CPU.
Architektura
- Harvardská - oddělená paměť programu (ROM) a paměť dat (RAM)
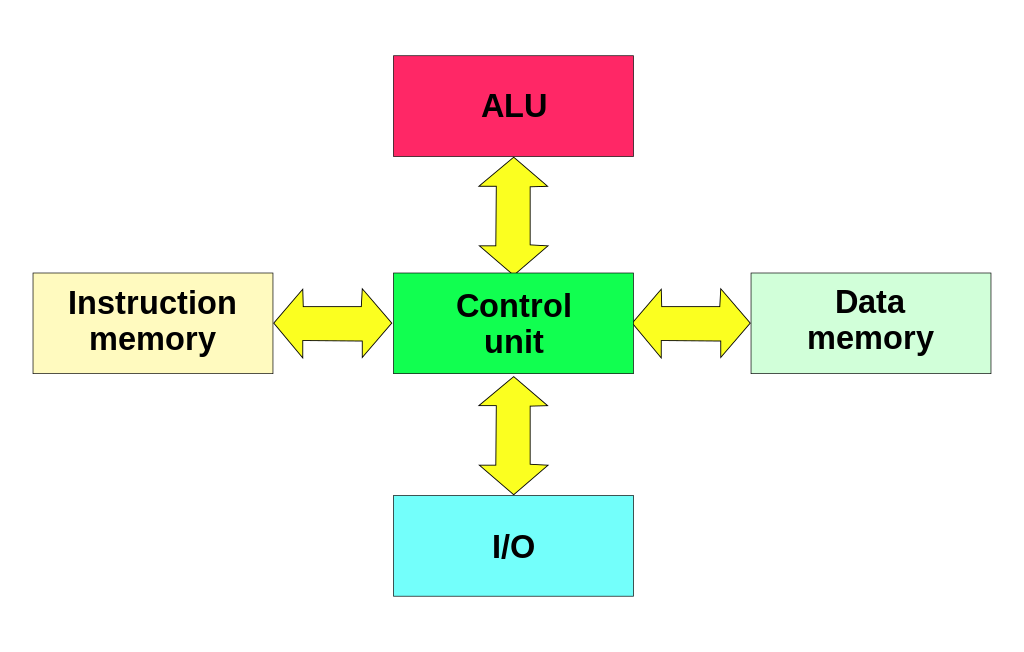
- Von Neumannova - sjednocená paměť (RAM)
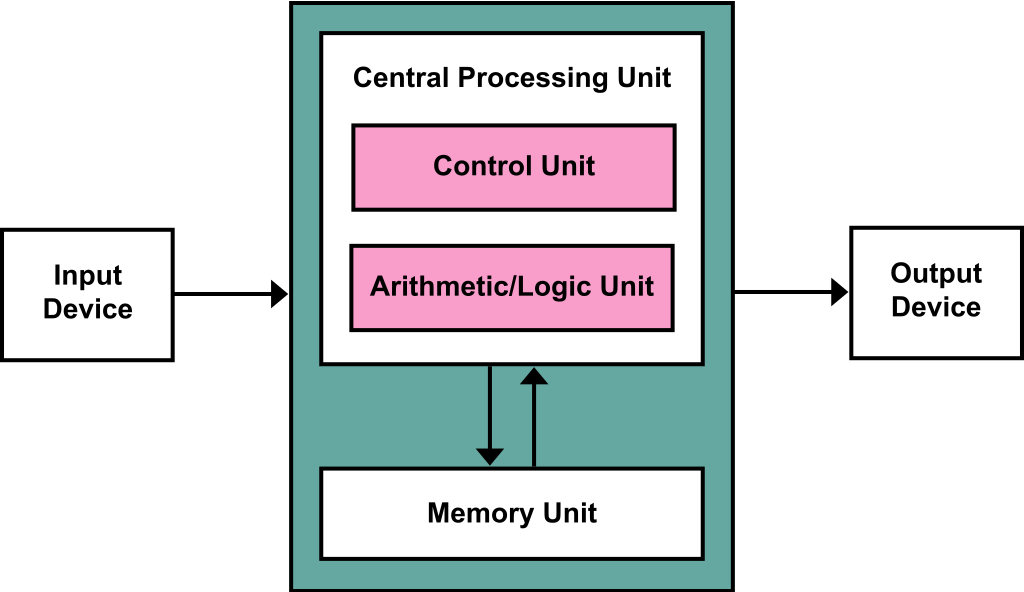
Náčrt
Doporučuji si načrtnout návrh vašeho CPU a podle toho se rozhodovat. Důležitý bod u vašeho návrhu CPU je kolika bitové jste dělali ALU. Pokud máte 8 bitové ALU, tak nemůžete mít 16 bitovou sběrnici (pokud něco nevyčarujete, možné je všechno...).
Navrhované šířky/počty
- Šířka adress v ROM
- Šířka hodnot v ROM
- Šířka adress v RAM
- Šířka hodnot v RAM
- Šířka instrukcí
- Počet registrů
- Šířka sběrnice
I/O (Vstup/Výstup)
Alespoň jeden vstup a výstup
Příkladné vstupy
- klávesnice (
Input/Output/Keyboard) - registr (
Memory/Register)
Příkladné výstupy
- Řada ledek (
Input/Output/LED) - HEX displej (
Input/Output/Hex Digit Display) - TTY (
Input/Output/TTY) - LED Matrix (
Input/Output/LED Matrix)
Instrukce
Vaše CPU by mělo mít několik vlastností:
- možnost spočítat libovolný početní problém
- libovolně pracovat s registry a pamětí
Zkráceně by mělo být, co nejvíce univerzální... Tohle je dobré mít v hlavě při návrhu instrukcí.
Instrukci si můžete rozčlenit jakkoliv chcete. U mého CPU jsem měl pouze OP code a ARGy, ale můžete do instrukce schovat různé flagy apod... (technicky vzato jsou to taky argumenty, ale pouze jednobitové :D)

V excelu pak vypadají instrukce nějak takhle

Doporučené konvence
{X}- libovolný registr X[X]- hodnota na adrese X
Doporučuji navrhnout v excelu nebo google sheets. Tabulka s jménem instrukce, krátky popis a její kód.
Typické instrukce jsou:
- mov {R1} {R2} - přesune hodnotu registru z R1 do R2
- movi {R1} 8b - přesune hodnotu v instrukci do R1
- add {R1} {R2} - sečte R1 R2
- jmp {X} - skočí na instrukci {X} v programu
- ...
Průběh exekuce instrukce
-
Fetch
- Načti hodnotu z instrukční paměti na adrese PC (Program Counter) do IR (Instruction Register)
- Přičti k PC jedna
-
Decode instruction
- Přečti IR, rozhodni se, zda potřebuješ další bity k instrukci
- Pokud ano, opakuj fetch, ale výsledek ulož do argument registrů,...
-
Execute instruction
- Podle toho, co je v IR, tak se zachovej
Vyžadované instrukce
Aritmetické
Instrukce, které se zabývají počty. Typicky vše co umí vaše ALU.
Příklady:
add A,B- přičti fixní registry A a B a výsledek ulož do Asub {R1},{R2}- odečti libovolné dva registry a výsledek ulož do R1shr {R1}- Proveď SHR operaci na libovolný registr R1 a výsledek ulož do R1
Paměťové
- Přesuny mezi registry (kromě interních jako např. program counter)
- Immediate data instrukce - instrukce, která vám dovolí nahrát libovolné číslo do registru
movi {R1} {8b number}- nahraje do libovolného registru R1 8 bitové číslo
- Práce s RAM - primárně načítání a ukládání z RAM
load {R1}- načtení hodnoty z adresy HL (dva fixní registry pro adresu RAMky) do libovolného registru R1store {R1}- uložení hodnoty z libovolného registru R1 do adresy HL
Control Flow
Jumpy v programu - rozdělují se na podmíněné a nepodmíněné
Nepodmíněné:
jmp {X}- jump na určitou instrukcijmpr {X}- jump na instrukci o X instrukcí dopředu či dozadu
Podmíněné:
jmpz {X}- skoč na X instrukci pokud je flagaZEROrovná jednéjumpr {X}- to stejné ale relativní jumpjmpc {X}- skoč na X instrukci pokud je flagaCARRYrovná jedné
Ostatní
- Typicky I/O
led- toggle na LEDku
CPU - Stavba
Doporučuji si CPU rozdělit na 5 částí:
- Registry - vnitřní paměti CPU
- CU (Control Unit) - něco co vaši instrukci přijme a podle toho vykoná kroky
- Control room - debug část pro čtení obsahů registrů a podobných věcí
- Input/Output - vstupy,výstupy...
- Paměť (RAM/ROM) - v harvardské architektuře typicky ROM pro program a RAM pro data, ve Von Neumannově architektuře pouze RAM
Hrdinské komponenty pro vaše CPU
Gates/Controlled Buffer- rozhoduje jestli pouštíte proud nebo ne, v parametrech navolíte pouze vstupní a výstupníData BitsWiring/Tunnel- komponenta pro přehlednost, vytvoříte n komponent se stejným labelem (Label) a bude vám přenášet vstup bez nutných kabelů přes celou plochuWiring/Probe- debug věc, pro zjištění hodnoty na kabelu...Memory/Register- nejpoužívanější paměťová buňka
Stepper
Stepper vám "stepuje" (krokuje) vaše instrukce. Jelikož některé instrukce zaberou více cyklů...
Jedná se o jednoduchý n-bitový counter s n-bitovým decoderem. Se vstupem CLK (Clock) a RST (Reset) a n-výstupy.
2 bitový stepper vypadá následovně:
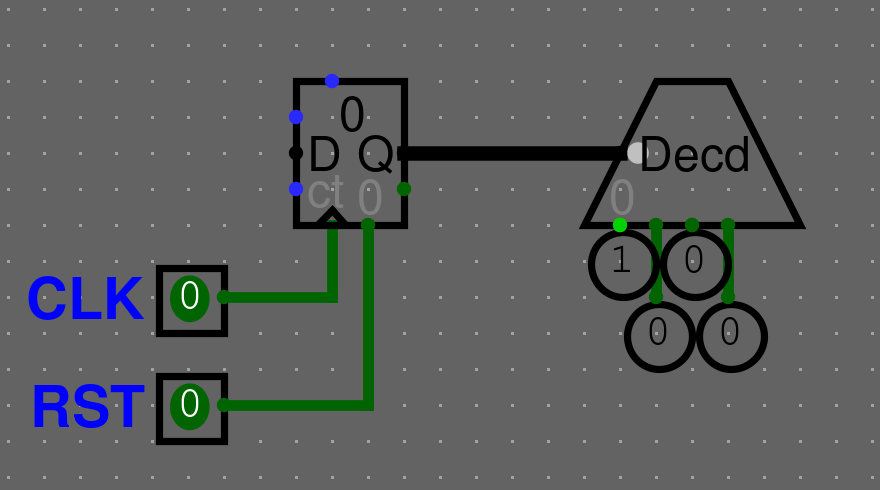
Registry
Ovládání registru může vypadat následovně
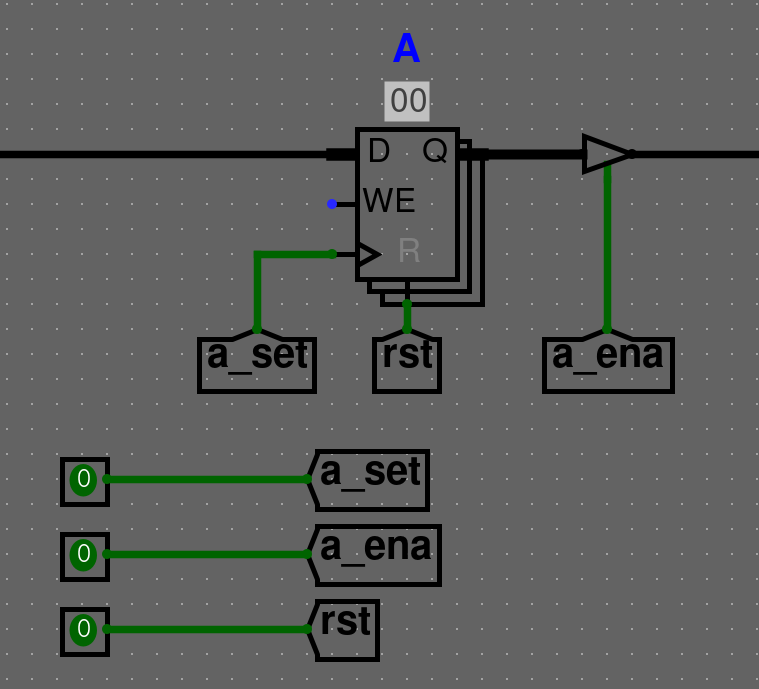
Velmi doporučuji použití tunelů (Wiring/Tunnel) a vytvořit konvence jako například <registr>_set apod..
Ovládání pro register A:
a_set- 1, když setujeme register Aa_ena- 1, když pouštíme register A na sběrnicirst- 1, když chceme provést reset registrů
Program Counter (PC)
Program counter je komponenta CPU, která vám říká, na jakém řádku programu (instrukce) se nacházíte. Potřebujete pro něj 2 věci:
- zvětšit o 1
- změnit hodnotu pro
jmp
Na obrázku jsou piny na ovládání, to je jen pro testování.
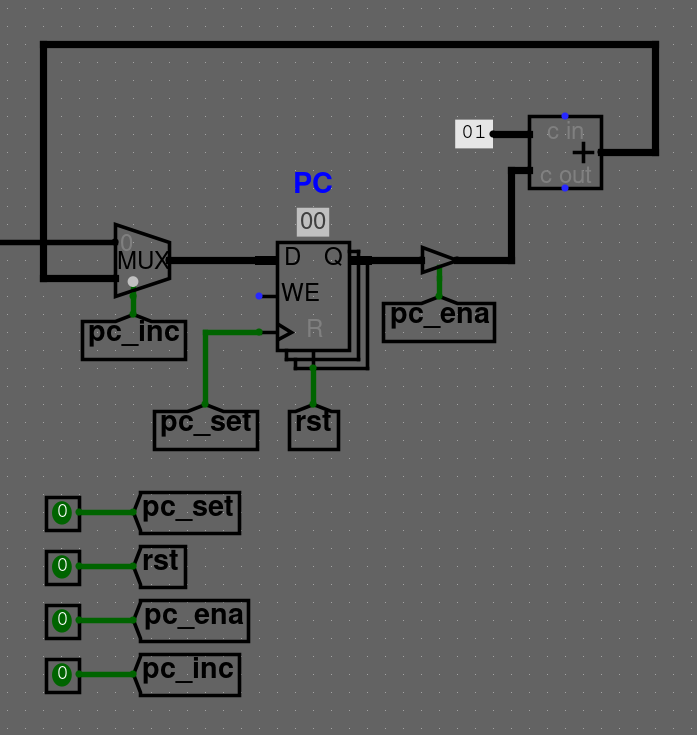
CPU - Programování
Od assembly k operačním systémům
Alexandr Pleskot (4.K 2024/25) ve spolupráci s Danem Bulantem v rámci svého maturitního projektu vypracoval článek, který pojednává o assembly, vztahu k C a operačnímu systému. Je to hezký úvod do programování v assembly, a následně přehled o tom, co je potřeba, aby na procesoru mohl bežet operační systém, což už je mimo obsah tohoto předmětu (my se spokojíme s tzv. "baremetal" mikrokontrolerem).
Od assembly k operačním systémům
Customasm
Velmi zkrácená dokumentace pro customasm...
Pro vaše CPU budete muset vytvořit example program. Velmi doporučuji webovou aplikaci customasm
- git - https://github.com/hlorenzi/customasm
- web - https://hlorenzi.github.io/customasm/web/
- wiki - https://github.com/hlorenzi/customasm/wiki
Jelikož má customasm svou vlastní dokumentaci, tak tuhle část projdu velmi zkráceně...
Subruledef
První si nadefinujeme podpravidla (typy) jako například registry apod.
#subruledef register
{
A => 0x0
B => 0x1
C => 0x2
D => 0x3
}
Ruledef (instrukce)
Zde nadefinujeme instrukce, viz. příkladná mv instrukce. Dejme tomu, že opcode pro mov instrukci je 1001 a šířka instrukcí je 16 bitů.
#ruledef
{
mv {src: register},{dst: register} => 0b1001 @ src`4 @ dst`4 @ 0x0
}
mv- název instrukce{src: register}- název parametru a typ, zde typ definovaný vsubruledefregister,- separátor{dst: register}- druhý argumentdst=>- operátor přepiš jako0b1001-0bznamená zapsáno v bitech a1001je opcode instrukce@- používá se jako separátorsrc`4- argument src zakóduj jako 4 bitovýdst`4- stejné0x0-0xhexdecimální zápis čísla0, pro doplnění do 16 bitů (naše šířka instrukce)
Dobré podotknout, že jako typ zde používám pouze register, ale velmi často použijete i další typy a to:
uXX- unsigned hodnotysXX- signed hodnotyiXX- signed nebo unsigned hodnoty
Programování
Typicky začnete program s start. Velmi doporučuji psát komentáře pomocí ;
start:
; přesune hodnotu z registru C do registru D
mv C,D
Celý example vypadá takhle:
#subruledef register
{
A => 0x0
B => 0x1
C => 0x2
D => 0x3
}
#ruledef
{
mv {src: register},{dst: register} => 0b1001 @ src`4 @ dst`4 @ 0x0
}
start:
; přesune hodnotu z registru C do registru D
mv C,D
Export do logisimu
Output Format: LogiSim 8-bitneboOutput Format: LogiSim 16-bitpodle šířky pamětiAssemble (Ctrl+Enter) >>- Zkopírujte výstup a uložte do
.txtsouboru - Klikněte na vaši
Memory/ROMkomponentu v logisimu - Klikněte u vlastnosti
Contentsna(click to edit) Opena vyberte soubor, kde jste si uložili výstup customasm
Poznámky z hodin
Tyto stručné poznámky v pár bodech shrnují probranou látku na hodinách týkajících se procesoru. Pro dosažení parity s látkou probranou na hodinách je potřeba si o každém zmíněném tématu něco přečíst.
25.2.2025: Princip procesoru
Témata z bakalářů:
- Úprava účelného sekvenčního obvodu na procesor, princip procesoru
- Návrh datové cesty pro procesor, překlad zdrojový kod - assembler - strojový kód - kontrolní signály, customasm
Výpisky:
- Procesor je plně synchronní sekvenční obvod, v každém cyklu provede nějakou jednu operaci na základě aktuálního stavu, tím vypočítá nový stav po provedení operace.
- Aby se jednalo o procesor, musí být obvod programovatelný, tj. sled operací jím prováděný je určený nějakým programem, který je uložený v nějaké programové/instrukční paměti.
- Procesor je "obecný", pokud na něm lze vypočítat libovolný spočítatelný příklad. Odborně se bavíme o Turingovské kompletnosti.
- V této paměti se nechází strojový kód - posloupnost instrukcí pro procesor v nějaké binární podobě, které procesor rozumí.
- Procesor si musí pamatovat, kde v programu se nachází, tj. kterou instrukci spustit jako další. Ukládá si to v tzv.
PC(Program Counter) neboIP(Instruction Pointer) registru. Tento registr obsahuje adresu příští instrukce v instrukční paměti. Typicky není uživatelsky přístupný, a s výjimkou skokových instrukcí se při provedení každé instrukce jednoduše zvětší. - Datová cesta procesoru umožňuje provést každou operaci, kterou má procesor umět, pomocí nějaké kombinace kontrolních signálů. Je možné, že některé komplexnější operace/instrukce budou vyžadovat více cycklů, protože datová cesta neumožňuje provést celou operaci najednou. Snažíme se počet cyklů držet nízký. Typické komponenty v datové cestě procesoru:
- 4-32 uživatelských registrů na mezivýpočty. Můžeme je např. zapojit tak, abychom mohli podle nějakých "adres" do jednoho z nich psát, a z libovolných dvou číst. Registry pak tvoří něco připomínající paměť s jedním zapisovacím a dvěma čtecími porty. Takové struktuře se pak říká "Registrová banka", někdy
GPR(General Purpose Registers). - ALU
- Datová paměť - na ukládání většího množství uživatelských dat, které se nevejdou do registrů
- Input/Output zařízení, resp. interface logika pro komunikaci s nimi.
- 4-32 uživatelských registrů na mezivýpočty. Můžeme je např. zapojit tak, abychom mohli podle nějakých "adres" do jednoho z nich psát, a z libovolných dvou číst. Registry pak tvoří něco připomínající paměť s jedním zapisovacím a dvěma čtecími porty. Takové struktuře se pak říká "Registrová banka", někdy
- Tyto kontrolní signály se z aktuálně prováděné instrukce vypočítají v tzv.
CU(Control unit, Kontrolní jednotka). Podle zvoleného kódování strojového kódu může být výpočet komplexní nebo triviální. - Máme následující abstrakce programu:
- Zdrojový kód v low-level programovacím jazyce (C, C++, Rust, Zig, Go...), ten se pomocí kompilátoru přeloží na:
- Jazyk symbolických instrukcí (assembler), jedná se o textovou a lidsky čítelnou reprezentaci programu. Každý řádek obsahuje jednu instrukci. Pomocí assembleru (programu co assembluje) se assembler přeloží na:
- Strojový kód, což je binární podoba programu, která už není lidsky čitelná. Instrukce můžou mít libovolný počet bitů, a to buď všechny stejný, nebo různý (variable-length instructions). Bez znalosti specifik kódování daného strojového kódu nelze určit, co daný program děla, kde která instrukce začíná, nebo zda se vůbec jedná o program nebo náhodné data. Program v této podobě se nahraje do instrukční paměti procesoru, který postupně instrukce čte a dekóduje je na:
- Kontrolní signály. Těmito procesor ovládá svoji datovou cestu, aby zajistil provedení té operace, kterou programátor určil.
- Assembler i strojový kód musí být dobře zdokumentovaný, aby bylo jednoznačně zřejmé, jaký program bude mít jaké chování v procesoru.
- Překlad z assembleru na strojový kód můžeme provádět ručně podle dokumentace - ta by měla obsahovat přesné rozložení bitů pro sestavení strojového kódu dané instrukce. Je to pracné a náchylné na chybu.
- Místo toho můžeme použít nástroje, např. napsat si vlastní assembler (program), nebo použít nástoj customasm, což budeme dělat my.
4.3.2025: Architektura souboru instrukcí
Témata z bakalářů:
- Architektura souboru instrukcí (ISA), návrhové parametry procesoru
- Typy architektur podle operandů, typy operandů instrukcí
Výpisky:
- ISA (Instruction Set Architecture) je kontrakt mezi návrhářem HW a vývojářem SW o tom, jak procesor funguje. Obsahuje vše, co je nutné zadefinovat:
- Množina instrukcí (jaké instrukce, s jakými operandy, jaké je jejich chování)
- Velikost dat, adres, operandů, instrukcí, etc.
- Typy operandů v instrukcích
- Kódování instrukcí (formát strojového kódu)
- Instrukce podle druhu:
- Aritmetické instrukce - provádí výpočet pomocí ALU
- Instrukce pro manipulaci s daty - přesun mezi registry, mezi registrem a datovou pamětí, načtení konstanty do registru...
- Instrukce pro řízení toku programu (skoky) - nepodmíněné a podmíněné skoky
- Speciální instrukce - nop, halt, IO, etc.
- Druhy operandů instrukce:
- Přímý (Immediate) - konstanta v instrukci, např.
addi r1, 3 - Registrový - číslo registru v instrukci, např.
add r1, r2 - Přímá adresa - v instrukci je adresa do paměti, instrukce pracuje s hodnotou v paměti, např.
add r1, [0x1234] - Registrový nepřímý (Indirect) - číslo registru v instrukci, v tom registru adresa do paměti, pracuje se hodnotou v paměti, např.
add r1, [r2]. - ... a další.
- Přímý (Immediate) - konstanta v instrukci, např.
- "Indirekce" = nemám hodnotu, ale mám adresu, kde ta hodnota je, pracuj s ní. Typicky se v assembleru značí nějakou formou závorek, e.g.
mov [r1], r2. - Strojový kód každé instrukce musí obsahovat:
- Operační kód = nějaký počet bitů, podle kterého procesor jednoznačně pozná, že je to tahle instrukce.
- Operandy instrukce.
- Pozn: Operační kód může a nemusí být pro všechny instrukce stejně dlouhý.
- Pozn: Operandy instrukce můžou a nemusí být v instrukci popřadě, dokonce můžou být jejich bity různě proložené, dokud je to pořadně zdokumentované.
- ISA podle komplexity a počtu instrukcí
- CISC - Complex Instruction Set Computer. Komplexní instrukce, které umí typicky provést výpočet a pracovat s pamětí zároveň. Velký počet instrukcí. Např. x86
- RISC - Reduced Instruction Set Computer. Malý počet jednoduchých jednoúčelových instrukcí. Aktuální trend ISA. Např. ARM, RISC-V, MIPS
- ISA lze podle schopností datové cesty procesoru a podle operandů ALU instrukcí rozdělit na různé kategorie:
- GPR load-store ISA, 3 explicitní operandy (source A, source B, destination). e.g.
add r1, r2, r3proveder1 = r2 + r3- Hodně univerzální, ale velké instrukce (3 explicitní operandy)
- GPR load-store ISA, 2 explicitní operandy (source A / destination, source B). e.g.
add r1, r2proveder1 = r1 + r2- Méně univerzální, ale menší instrukce - dobrý trade-off
- Akumulátorová ISA, 1 explicitní operand (source A / destination je vždy akumulátor, udáváme pouze source B), e.g.
add r2provedeACC = ACC + r2- lze zafixovat i source B a mít 0 explicitních operandů
- malé instrukce, ale malá flexibilita - pro každý výpočet musíme manipulovat s daty z/do ACC -> pomalé, nepřehledný assembler
- Zásobníková ISA - místo GPR máme zásobník. 0 explicitních operandů, operandy jsou vždy 2 horní prvky zásobníku a výsledek se ukládá na zásobník.
- V hardwaru obsolete, ale v SW se používá např. uvnitř JVM.
- GPR register-memory ISA - jeden/více source/destination operandů může jít z datové paměti
- Typické pro CISC procesory - komplexní, pomalé.
- GPR load-store ISA, 3 explicitní operandy (source A, source B, destination). e.g.
- Mezi těmito varianty se rozhodujeme podle toho, co je pro nás jako návrháře CPU důležité:
- Rychlost procesoru - počet cyklů per instrukce, maximální hodinová frekvence, čekání na paměť, etc.
- Počet hradel (jednoduchost procesoru)
- Velikost instrukcí - menší kód se rychleji načítá a tak v praxi beží rychleji. Alternativně, do stejnbé paměti se nám vejde komplexnější program.
- Komplexita programování v assembleru (pokud máme compiler, tak nás tento bod moc nezajímá, viz x86)
- Naší prioritou by měla být jednoduchost programování v assembleru (smysluplné jednoduché instrukce) a jednoduchost instrukcí (jednoduchá implementace v jediném cyklu).
11.3.2025: Zrušeno
25.3.2025: Návrh ISA, Obecnost procesoru
- Adresní režimy (pokračování), implementace (všech) adresních režimů v datové cestě
mov R1, [R1 + R2*d + c]- přístup do pole struktur (Cstruct) ke konkrétní položce (field) struktury. Bežné na CISC- ořezané varianty toho adresního režimu, e.g. pouze
+c
- ořezané varianty toho adresního režimu, e.g. pouze
- postinkrement, predekrement - ekvivalent
a = arr[i++]aa = arr[--i]v C. Implementováno v HW paralelně s paměťovým přístupem. Nutné pro hardwarovoou podporu zásobníku, tedy instrukcípushapop - x86 instrukce
lea, a jak se komplexní adresní režim na x86 "zneužívá" k bežným výpočtům (které s adresou nebo pamětí nemusí mít nic společného)
- Adresní režimy jsou vlastností datové cesty procesoru, každý parametr každé instrukce podporuje některé adresní režimy, ne nutně všechny
- Operace, které musí jít nutně provést na obecném procesoru (ne nutně pomocí jediné instrukce):
- [ALU] provést ALU operaci na libovolných datech v CPU (registry, paměť, immediate v instrukcích neboli konstanty v kódu)
- [move] přesun (kopírování) dat mezi libovolnými registry
- [load/store] přesun dat do/z paměti z/do libovolného registru na vypočtenou adresu (tj. adresu z e.g. registru)
- můžou být též implementovány jako varianty move instrukce, pokud v ní je místo na pár bitů na rozlišení - mají totiž podobnou sadu operandů
- [load imm] načtení konstanty (tj. dat z instrukcí) do libovolného registru
- [jump] skok (změna PC) na vypočtenou adresu (tj. e.g. z registru)
- může být např. vynechán pokud lze realizovat move instrukcí
- [cond] podmíněné spuštění (příští) instrukce
- může být realizováno jako podmíněný skok (bežné), ale nemusí - je to ekvivalentní přeskočení příští instrukce, pokud příští instrukce je jump
- přeskočení příští instrukce může být komplikované, pokud jsou instrukce variabilní délky - potom pomáhá mít v instrukci její délku
- podmínky: lt, gt, eq, zero, sign (negative), overflow
- konkrétní realizace není specifikovaná
- typicky každý flag výstup z ALU by měl jít použít jako podmínka
- operandy pro porovnání nebo test můžou být specifikovány v instrukci, nebo může být použit výsledek z předchozí (např. ALU) operace
- je potřeba umět vyhodnotit podmínku i její opak
- e.g. opak od je
- nemusí to být implementováno v HW, protože v assembleru půjde podmínky invertovat tím, že podmíněným skokem "přeskočíme jump instrukci" na kód pro opačnou podmínku
- alu záporné varianty instrukcí (jz -> jnz, jeq -> jne) zjednodušují při programování v assembleru uvažování o podmínkách. Instrukce lze realizovat též jako pseudo-instrukce v assembleru
- [io] musí jít komunikovat s input a output zařízeními - různé způsoby, je jedno jak
- Ne vsechny tyto operace musí být na procesoru přímo proveditelné v jedné instrukci - stačí když lze provést pomocí několika instrukcí (tuto skutečnost budete na vašem CPU muset demonstrovat)
- Je tedy možné některé instrukce "omezit" (zafixovat některé z jejich operandů, nebo některé instrukce pro některé adresní režimy vůbec neimplementovat), pokud lze toto omezení "zrušit" použitím posloupnosti jiných instrukcí procesoru
- Např:
- ALU instrukce nemusí umět brát immediate, pokud umí brát registr, a do registru lze jinak načíst immediate
- Opačně (např. v RISC-V): Nemusíme mít instrukci typu load imm, pokud umíme ALU operaci s nulovým registrem a immediate
- Práci s paměti nemusí jít provést nad libovolnými registry, pokud umíme mezi registry hodnoty přesouvat
- Opačně (ale nepraktické): Nemusíme umět přesouvat mezi registry, pokud umíme libovolný registr uložit+načíst z paměti
- Jump může jít realizovat jako move do (v tomto případě nutně uživatelského) registru PC.
- Pořád je potřeba nějak řešit podmínky. Příklad pro tuto variantu může být např. instrukce, která podle podmínky zabrání spuštění příští move instrukce (tedy i jumpu, a jump je schopen přeskočit libovolné instrukce => naplnili jsme požadavek "podmíněné spuštění instrukce").
- Pokud v instrukci není dost bitů pro všechny nutné operandy, lze instrukci rozdělit na dvě instrukce "přípavu" a "dokončení" operace. Procesor si parametry z přípravy zapamatuje do speciálních registrů a použije je při dokončení
- Např. načíst 16bit immediate, pokud instrukce jsou 16bitové, lze realizovat dvěmi instrukcemi: load high 8 bits, load low 8 bits
- Pokud datová a instrukční paměť jsou ta samá paměť (u některých CPU je a u některých není), není load imm vůbec potřeba - načíst konstantu lze jednoduše pomocí move instrukcí se správnou (předem známou) adresou
- ALU instrukce nemusí umět brát immediate, pokud umí brát registr, a do registru lze jinak načíst immediate
- Je vhdoné zvolit nějaký kompromis mezi:
- Počtem instrukcí
- Komplexitou implementace instrukcí v HW
- Množstvím a velikostí operandů s ohledem na zvolenou velikost instrukce
- Přidanou komplexitou při programování v assembleru (přesouvání dat, atypické skokové struktury, etc.)
- Počet nutných instrukcí pro bežně používané operace (klasické C konstrukty jako for loopy, if-else, práce s array a strukturami, etc.)
- Ovlivňuje rychlost procesoru i velikost kódu
- konec středeční skupiny
- Mapování instrukcí do strojového kódu
- Nejjednodušší způsob - fixně velký (e.g. pro procesor se 14 instrukcemi minimálně 4 bity) tzv. "opcode" (operační kód) na začátku instrukce, který přesně identifikuje typ instrukce
- (výhoda) Dekódování instrukci (zjištění ze strojového kódu, o kterou instrukci se jedná) lze pak v HW realizovat jednoduše dekodérem
- (nevýhoda) Každá instrukce má k dispozici stejný počet bitů na operandy - některým instrukcím to nemusí stačit, pro některé to může být zbytečně moc
- Instrukce, kterým to nestačí, se musí ořezat, rozdělit na dvě instrukce, nebo začít zabírat dvě adresy (variabilní délka instrukcí přidává komplexitu), nebo se musí zvětšit všechny instrukce (ještě víc wasted místa v ostatních instrukcích)
- Do nevyužitého prostoru v instrukcích se ale můžou přidat bity upřesňující variantu/režim/chování instrukce, např:
- load a store a move můžou být pouze varianty jedné univerzální move instrukce - berou totiž podobné operandy - jednodušší dekódování+datová cesta
- jump instrukce může obsahovat 1 bit pro každou možnou podmínku - pokud je 1, skočí se pouze, pokud je podmínka splňená. Samé nuly => nepodmíněný skok
- V případě chytrého použití variant instrukcí počet různých instrukcí (a případně nutná šířka opcode) rapidně klesá - jednodušší implementace
- Jiný způsob - VLSM - operační kód je pro každou instrukcí různě dlouhý, ale mezi sebou se nepřekrývají
- Instrukce s velkým počtem operandů mají krátký opcode - takových může být málo
- Instrukce s malým počtem operandů mají delší opcode - může jich být víc
- Stejný princip jako Variable Length Subnet Mask v sítích
- Pro 8bit instrukce (bez variabilní délky instrukcí) v podstatě nutnost
- Na příští hodině detaily
- DÚ (TBA): Sestavit si vlastní ISA splňující tyto kritéria s nějakou zajímavostí, inspirovat se dá na stránce s jednoduchými ISA.
1.4.2025: Návrh blokového diagramu CPU
Konkrétně návrh blokohového diagramu jednocyklového procesoru podle zvolené instrukční sady.
Postup návrhu:
- Projít si všechny instrukce, jejich chování, uvědomit si, s jakými daty pracují, jaké jednotky (ALU, etc.) používají, a kam ukládají výsledek.
- Pro každou kombinaci chování musí procesorem existovat fyzické cesty, kterými data mohou téct, aby provedli danou operaci, jinak procesor nebude jednocyklový
- Umístit do blokového designu všechny moduly, které budou v procesoru potřeba, označit jejich vstupy a výstupy, včetně kontrolních signálů a clocku
- GPR (general purpose register file), s nějakým počtem zapisovacích a čtecích portů, podle potřeb ISA
- ALU
- Datovou paměť
- Instrukční paměť, PC registr, CU (control unit, kontrolní jednotku)
- Separátní instrukční a datovou paměť máme, aby šly paměťové instrukce načíst a provést v jediném cyklu. V případě sjednocené paměti bychom museli v jednom cyklu načíst instrukci, a pak až v dalším cyklu provést paměťovou operaci
- Na každém vstupu každého modulu budeme možná potřebovat pro různé instrukce přivést jedny z více různých dat (z různých míst v procesoru)
- Tento problém výběru N z 1 můžeme vyřešit přidáním kontrolního signálů, který řídí, která z hodnot se vybere, a komponenty, která podle tohoto signálu umí výběr provést
- Není problém tohle udělat pro každý ze vstupů, i pokud nakonec zjistíme, že tam byla potřeba pouze jední hodnota, a výběr tedy nebylo potřeba řešit - stačí výběrový řídící signál zafixovat na konstantní hodnotu (všechny syntézní nástroje toto vyoptimalizují na přímé spojení drátů).
- Pro každou instrukci projdeme tok dat, který zkrz CPU vyžaduje, a přidáme do možného výběru daných vstupů dráty s daty, které tam instrukce potřebuje.
- ie. chceme-li kopírovat z libovolného registru do libovolného registru - musí jít přivést čtecí výstup z GPR do zapisovacího vstupu GPR
- Je výhodné při kreslení diagramu používat "tunely" / "labely drátů" - pokud dva dráty na různých místech stejně pojmenujete, chápou se jako spojené.
- Zredukujete tím šum z množství drátů, a zároveň tím diagram lépe zdokumentujete, protože každý drát smysluplně pojmenujete
- U každé komponenty dbejte na označení a pojmenování všech kontrolních signálů. Tyto signály nejsou potřeba nikam připojovat, předpokladá se, že je generuje CU.
- Každá sekvenční komponenta musí mít symbol clock inputu, není potřeba ho nikam zapojovat, všechny clocky se chápou spojené
- Pozor na to, že každá instrukce (vyjma úspěšných skoků) musí implicitně zvětšit PC, aby se v příštím cyklu spustila následující instrukce. Bez této funkcionality bude procesor opakovaně spouštět pouze první instrukci, nespustí tedy program, tedy není programovatelný, tedy to není procesor!
- Zapojení IO instrukcí silně závisí na jejich konkrétní variantě, nicméně vždy platí, že budou vysílat nějaké hodnoty mimo procesor, nebo je přijímat z vnějšku. To můžeme označit např. použitím kraje papíru jako hranice modulu procesoru, nebo pomocí symbolu , kterým označíme fyzický pin procesoru jako reálného integrovaného obvodu (ie. drát co z něj vede ven)
- Kde v CPU se tyto odchozí hodnoty berou, nebo kam se mají příchozí hodnoty v CPU uložit, je zřejmé z instrukce, a podle toho je potřeba upravit datovou cestu
- Jednobitové statusové IO signály se vypočítají v CU (jde o kontrolní signály) pokud jde o výstupy, nebo slouží jako vstupy do CU (jde o stavové/statusové signály) pokud jde o vstupy. Zejména
- e.g.
out_valid, který navenek signalizuje, že CPU chce odeslat (validní) hodnotu - e.g.
in_valid, který procesoru zvenku udává, že je k dispozici hodnota, kterou input instrukce může přečíst - e.g.
in_acknowledge, kterým procesor indikuje, že hodnotu na vstupu zpracoval a odesílatel ji může přestat vysílat
- Žádný modul nelze v jednom cyklu použít na dva různé účely zároveň.
- Statusové výstupy z ALU (a klidně další) je potřeba uložit, aby s nimi mohly příští instrukce pracovat. Těmto hodnotám a registru kam je uložíme, se říká příznaky (flags)
- Může být jeden N-bit flag registr, nebo N jedno-bitových registrů (pro N flagů), není v tom rozdíl. Zvolte, s čím se vám bude v kontextu vybraných instrukcí lépe pracovat
- Ne všechny instrukce způsobí uložení flagů, obecně by se měly uložit pouze ty flagy, které nebývají v tomto cyklu smysluplné hodnoty. Např. při operaci xor se nastaví zero a sign ale ne carry, protože neexistuje smysluplná hodnota carry ve výsledku operace xor. Pro zjednodušení může např. ALU operace přepsat všechny flagy, ale ostatní instrukce ne.
- Nezáleží na podobě konkrétní implementace, ale záleží na tom, aby bylo zvolené chování zdokumentované. V momentě, kdy je chování zdokumentované, nemůže být "špatně" - je to to co jste vy jako návrhář zvolili, a je zodpovědností programátora se tomu přizpůsobit. Procesor ale musí stále být obecný.
- Flagy se používají na různých místech, např. CU je potřebuje pro rozhodnutí o podmínkách skoků, a ALU bude svůj CIN brát také z flagů. Nezapomeňte tyto skutečnosti v diagramu naznačit - pokud CU nemá vstup "flags", který má hodnotu z flag registru, nemá podle čeho o skoku rozhodnout!
- Kontrolní jednotka má jako vstup aktuální instrukci, a jako výstup případné dekódované immediate hodnoty. Ale má i spoustu dalších vstupů a výstupů z následujících dvou kategorií:
- Kontrolní signály (výstupy) - řídí konfiguraci datové cesty. Nemusíte je u CU uvádět jako výstupy explicitně, stačí naznačit pár výstupů a nadepsat "control signals" nebo podobně. Předpokládá se, že všechny pojmenované non-driven dráty (bez nějakého zdroje signálu) jsou kontrolními signály a generuje je právě CU.
- Stavové (status) signály (vstupy) - další informace o stavu datové cesty, které CU potřebuje k rozhodování. Sem patří např. flagy,
in_validz IO, případný signáldonez např. sekvenční násobičky v ALU, na kterou se musí počkat, etc.
- Kontrolní jednotka umí dekódovat instrukci, můžeme jí pověřit kromě generování signálů i dalšími vypočetními úkoly, které s dekódování instrukce souvisí, např.:
- Extrakce immediate argumentů z instrukce spravným způsobem (dle typu instrukce)
- Vypočítání nové hodnoty flagů, pokud je potřeba flagy instrukcí přímo upravit (tj. ne nepřímo výpočtem z ALU)
- Každý vodič má vyznačenou velikost - pokud má CPU 16-bit data, bude velká část vodičů 16bit, avšak ne všechny. Např. vstup a výstup flag registru, immediate hodnoty z instrukce, a další budou mít jinou velikost
- Nelze spojit vodiče dvou různých šířek - taková operace je nejasná, nespecifikuje, co se zbylými dráty. Je potřeba provést konverzi.
- Konverze mají několik typů podle hodnot, nad kterými pracují. Rozlišujeme zvětšení / zmenšení podle velikosti, a signed / unsigned podle typu dat na drátě.
- Zvětšení:
- Unsigned: hodnotu interpretujeme jako číslo bez znaménka, stačí tedy na MSB straně hodnotu rozšířit nulami (Zero Extend), a hodnota zůstane zachovaná.
- Signed: hodnotu interpretujeme jako číslo se znaménkem v dvojkovém doplňku, tj. při rozšíření musí zůstat znaménko i hodnota čísla zachovaná. Nestačí rozšířit nulami - to by vždy vytvořilo kladné číslo, ještě ke všemu jiné hodnoty. Na první pohled se to zdá komplikované, ale tato konverze se dá implementovat jednoduše: rozšíříme hodnotu na MSB straně čísla nikoliv nulami, ale hodnotou znaménka čísla (tedy hodnotě MSB). Tedy z čísla
SXXXXXXXudělámeSSSSSSSSSXXXXXXX, kdeSje sign bit čísla aXXXXXXXje zbytek čísla. Např. rozšíření 4-bit hodnoty =1110na 8-bit vytvoří hodnotu11111110, což je v 8-bit dvojkovém doplňku pořád . Tento postup funguje i pro kladné čísla, kdeS=0. Tomuto postupu se říká Sign Extend.
- Zmenšení:
- Unsigned: Jednoduše zahodíme MSB bity. Pokud některý z nich byl 1 (lze spočítat hradlem OR pokud je to potřeba), znamená to overflow - hodnota nebude stejná jako vstup, a nelze s tím nic dělat. Výsledná hodnota bude mít hodnotu , kde je vstupní hodnota a je počet bitů výsledku.
- Signed: Chceme zachovat znaménko čísla. Oddělíme tedy sign bit
Sod zbytku čísla. Zbytek čísla zmenšíme postupem pro unsigned číslo na bitů, a před výsledek vrátíme sign bitS, čímž cískámeN-bitové číslo. Výsledek bude mít hodnotu .
8.4.2025: Mapování instrukcí do strojového kódu
- První krok - projít instrukční sadu, určit velikosti všech operandů podle hodnot, které se do nich musí vejít
- Tyto velikosti per instrukce sečíst -> celková velikost operandů instrukce
- Metoda "fixně velký opcode": opcode bude mít fixní počet bitů tak, aby měl dost hodnot pro celkový počet instrukcí
- Identifikovat instrukci s největší celkovou velikostí operandu - takto velký bude operand pro všechny instrukce
- Podle počtu instrukcí (s případnou budoucí rezervou) zvolit velikost opcode
- Formát instrukce:
<opcode><operands>- pro všechny instrukce stejné velikosti (jak jsem je zvolili v předchozích dvou krocích) - Menší instrukce budou obsahovat nevyužité bity (neefektivní) - doporučuji je zadefinovat jako
0 - Lehké přidávání instrukcí, a přidávání operandů do instrukcí, ve kterých je místo
- Možnost "sloučit" instrukce s podobnými operandy do jedné a přidat operand, který mezi nimi rozhoduje (stejný princip jako u obecné "alu instrukce", která má ALU opcode jako jeden z operandů). E.g. load a store můžou být jedna load/store instrukce, kde jednobitový operand rozhoduje o směru přenosu
- Tím se dá zredukovat počet instrukcí a případně velikost opcode - plus se víc efektivně využívá prostor na operandy
- Nevýhoda - větší instrukce, počet bitů nejspíš nebude dělitelný 8 (horší práce se strojovým kódem na konvenčních počítačích, e.g. při psaní compileru)
- Možnost zaokrouhlit velikost instrukce nahoru na násobek 8 - "padding" bity zadefinujte jako
0. Víc neefektivní, ale "normálnější"
- Možnost zaokrouhlit velikost instrukce nahoru na násobek 8 - "padding" bity zadefinujte jako
- Metoda "variabilně velký opcode" pomocí VLSM (Variable-Length Subnet Mask), tutoriál
- Seřadit instrukce od největšího operandu po nejmenší
- Identifikovat maximální velikost operandu, a počet instrukcí s touto velikostí (běžně bude jedna, někdy dvě)
- Zvolit minimální velikost opcode tak, aby se do něj vešlo počet největších instrukcí + 1 hodnot. Pokud je jenom jedna, stačí jediný bit.
- Velikost instrukce: minimální velikost opcode + velikost největšího operandu. Většinou tedy velikost největšího operandu + 1.
- Formát instrukce:
<opcode><operands>ALE:- operands jsou vždy na konci instrukce a přesně tak velké, jak je potřeba (pro různé instrukce různě)
- opcode vyplní zbytek instrukce - klidně celou instrukci, pokud nemá žádné operandy
- variabilně velký opcode tvoří jakýsi "prefix" s určitou délkou, který unikátně identifikuje tuto instrukci
- zbytek instrukce po tomto prefixu jsou operands, které se jakoby předávájí této instrukci pro zpracování
- Tyto části lze přirovnat k částem adresy sítě v routovací tabulce (PSI): opcode je adresa sítě, operands je adresa zařízení uvnitř sítě
- Velikost opcode odpovídá velikosti síťového prefixu v zápisu takové adresy: 10.0.1.2/8 má 8bit prefix (síť, opcode) a zbytek 24b adresu (zařízení, operands)
- Největší instrukce bude nejspíš
/1, někdy/2, pokud jich je více
- Vyplňujeme tabulku ve formátu
<opcode><operands>, kde sloupce jsou bity instrukce a řádky jsou jednotlivé instrukce - Od největší instrukce postupuje postupně a pro každou instrukci:
- Na novém řádku vyznačíme její název, ve sloupcích bitů instrukce vyznačíme (od LSB) všechny operandy instrukce
- K názvu doplníme i asm podobu instrukce a dokumentaci chování instrukce (pokud je plbá dokumentace jinde, stačí stručně)
- Tyto bity se předpokládá že můžou nabýt libovolných (legálních v rámci požadavků konkrétní instrukce) hodnot
- Zbylé bity (směrem od MSB) tvoří opcode. Opcode každé instrukce je konstanta, podle které musí CU být schopna instrukci jednoznačně poznat (stejně jako router musí jednoznačně vědět, do které sítě má paket nasměrovat)
- Jako opcode můžeme zvolit libovolné bity tak, aby nenastala kolize s žádnou jinou instrukcí, která už v tabulce je.
- Doporučuji začínat od nuly a pak binárně počítat nahoru - budete mít v mapování a v opcodech větší pořádek, a instrukce budou seřazené vzestupně podle opcodu
- Podmínka zabránění kolizím: Pro libovolný pár instrukcí musí platit:
- Vezmeme menší z délek jejich prefixů (tj. pokud se jedná o instrukce s prefixem délek
/3a/5, bereme3) a nazveme hodnotuN - Pokud porovnáme prvních
Nbitů obou instrukcí, nesmí se rovnat (musí se lišit alespoň v jednom bitu)- V opačném případě je menší instrukce "subnet" té větší, tj. tu menší jste namapovali přes už existující hodnoty strojového kódu té větší! CU neumí mezi těmito instrukcemi rozlišit!
- Bity pro opcode vybírejte v souladu s touto podmínkou, zároveň doporučuji průběžně podmínku kontrolovat, pokud si nejste mapováním jistí.
- Vezmeme menší z délek jejich prefixů (tj. pokud se jedná o instrukce s prefixem délek
- Více informací najdete v libovolném návodě na VLSM, e.g. tutoriál
- Tato metoda předpokládá, že znáte celou sadu instrukcí předem, a vytvoří velmi efektivní mapování s minimálním možným počtem bitů, a nejspíše v něm zůstane spousta dalšího místa na spoustu dalších malých instrukcí.
- Stejně jako u VLSM se může stát, že pokud později budete chtít přidat velkou instrukci, nenajdete na ní místo. To lze vyřešit přemapováním instrukcí od začátku (címž to může vyjít jinak a lépe) nebo přidáním dalšího bitu před začátek instrukce, čímž se zdvojnásobí prostor v instrukci, a vaše nová instrukce se tam pak garantovaně vejde.
- Vlivem toho, jak mapování funguje, skončí podobné instrukce (load, store, etc.) s podobným layoutem operandů a podobným opcodem (možná se budou lišit o jediný bit!). Máme tedy "zadarmo" výsledek techniky "slučování instrukcí", nemusíme pro to nic extra dělat.
- Na novém řádku vyznačíme její název, ve sloupcích bitů instrukce vyznačíme (od LSB) všechny operandy instrukce
- Obecné tipy pro mapování instrukcí:
- Mapování provádějte jako tabulku v excelu, vytvořte si podmíněné formátování buněk s bity tak, aby e.g. 0 byla červená a 1 zelená.
- Do této tabulky můžete zároveň vložit dokumentaci k instrukcím - bude pak úplně postačovat jako příručka k instrukční sadě procesoru
- Spolu s blokovým diagramem datové cesty CPU, a stručným popisem sady registrů, pamětí, velikostí, etc. tvoří kompletní dokumentaci k CPU. Dokumentace je nedílnou součástí závěrečného projektu.
- Snažte se, aby podobné druhy argumentů (destination register, 8bit immediate, flags, etc...) byly v co nejvíce instrukcích na tom samém místě - např. pokud je imm8 vždy na konci instrukci, stačí z CU vyvést těchto 8 bitů jako immediate, nemusíte pro extrakci tohoto immedate z instrukce vůbec řešit, o jakou instrukci jde. Pokud bude potřeba, použije se, a bude správně, jinak se nepoužije.
- Mapování provádějte jako tabulku v excelu, vytvořte si podmíněné formátování buněk s bity tak, aby e.g. 0 byla červená a 1 zelená.
- Implementace dekódování instrukce jako obvodu:
- Chceme z efektivně zakódované instrukce získat informaci o tom, o kterou instrukci se jedná, a to v kódování "1 z N".
- To znamená uvnitř CU chceme mít 1 vodič pro každou instrukci, a aby daný vodič byl true pouze a pouze pokud spouštíme tuto danou instrukci (tj. všechny ostatní musí být false).
- Varianta "fixní velikost opcode" - dekodér.
- Varianta "variabilní velikost obcode" - parallel decision tree:
- Pro každou instrukci potřebujete ověřit že nějakých X počátečních bitů instrukce má nějakou konstantní hodnotu
- Tak pro každou instrukci vytáhneme správný počet bitů z instrukce, a provedeme porovnání s konstantou
- Porovnání s konstantou může být optimalizovaná varianta 1 více vstupový AND se znegovanými vstupy (jako mintermy uvnitř dekodéru!)
- Nebo prostě komparátor a konstanta (pozor, ta je v hexadecimální soustavě, a pozor na správné velikosti!)
- Na optimalitě tohoto obvodu nezáleží, na zjednodušování obvodu máme nástroje. Jde hlavně o to popsat chování obvodu co nejsrozumitelnějším, přehledným a udržitelným způsobem!
- Můžete pro účely optimalizace zapojení recyklovat některé vodiče, např. definovat instrukci na základě toho, že to není jiná instrukce AND nějaké bity z instrukce - pouze tam, kde to zjednoduší obvod.
- Chceme z efektivně zakódované instrukce získat informaci o tom, o kterou instrukci se jedná, a to v kódování "1 z N".
- Zbytek CU potom má jediný úkol: Každý "instrukční" signál, který jsme vygenerovali dekódováním instrukce, "rozsvítí" přesně ty sadu kontrolních vodičů, které jsou potřeba pro provedení instrukce. Protože všechny ostatní instrukční signály budou "mlčet", můžeme požadavky na kontrolní signály od všech instrukčních vodičů jednoduše ORnout.
15.4.2025: Zapojení kontrolní jednotky, Vstupy a výstupy CPU
- Dekódování instrukcí viz minulý týden
- Jakmile máme dekódovaný typ instrukce ve formátu 1 z N, musíme z této reprezentace vypočítat všechny kontrolní signály, tj:
- Jednobitové kontrolní signály (všechny WE, dvouvstupové muxy, ovládání IO, etc.)
- Předpokládáme výchozí stav kontrolního signálu (pokud potřebujete , invertuje kontrolní signál a postupujte stejně)
- Poté stačí aby ty dekódované instrukční signály, které daný kontrolní signál potřebují v nevýchozím stavu, ho přinutili do žádoucího stavu
- Stačí tedy ORnout všechny "požadavky" na nevýchozí hodnotu
- Případně můžete na kontrolním signálů provádět další výpočty, pokud je to potřeba (e.g. podmínky jumpu)
- Vícebitové kontrolní signály (výber registrů v GPR, selector signály větších multiplexorů)
- Zde chceme na výstup kontrolního signálu přivést jednu z N hodnot (některé bity instrukce, jiné bity instrukce, konstanta, hodnota z registru nebo IO, etc.)
- Mezi všemi variantami rozhodujeme multiplexorem - nyní stačí spočítat selector tohoto multiplexoru, typicky 1-3 bity
- Každý z bitů selektoru považujeme za samostatný kontrolní signál - použijeme metodu pro jednobitové kontrolní signály tak, aby každá instrukce navodila přesně tu kombinaci bitů selektoru tak, aby multiplexor vybral příslušnou hodnotu.
- Existují i alternativy, např. postavit vnitřek multiplexoru bez dekodéru - v předchozím bodě de facto implementujeme encoder, jenom abysme pak hodnotu poslali do multiplexeru, tedy do dekodéru uvnitř něj. Tuto zbytečnou encoder-decoder cestu můžete vynechat tím, že si postavíte vlastní MUX, který přímo bere selector v podobě . Musíte pak ale zaručit, že neporušíte kódování - jinak dostanete na výstupu multiplexoru divné hodnoty.
- Jednobitové kontrolní signály (všechny WE, dvouvstupové muxy, ovládání IO, etc.)
- Vstupy a výstupy procesoru
- Výběr z IO komponent implementovaných v Logisimu - procesor musi mít "zajímavé" a "uživatelsky" přívětivé IO na plný počet bodů
- Doopravdy: Vstupy a výstupy existují mimo procesor, a jsou k němu připojené pomocí fyzických pinů procesoru
- Zjednodušení pro nás: IO stavíme uvnitř procesoru, na stejné úrovní, aby bylo jednodušší procesor debuggovat, ALE:
- IO musí být na jednom místě pohromadě a být k procesoru připojené pomocí tunelů, jako kdyby CPU bylo samostatný modul (vizuálně).
- Této sekci obvodu o velikosti jedné obrazovky říkáme "Control room", a musí v ní být kompaktním a přehledným způsobem vizualizované:
- Všechny IO a jejich ovládací prvky (již zmíněno)
- Hodnoty všech registrů CPU, včetně interních! (stačí pod sebou tunely a hexa nebo decimální probes - tunel tvoří popisek a probe hodnotu)
- Indikace aktuálně spouštené instrukce - buď číslo a k němu legenda nebo sada popsaných LED (signály k nim už máte v CU)
- Důležité operandy: Pro ALU instrukci alu opcode, pro mov instrukci číslo src a dst registru, etc.
- Hodnoty flagů - stejným způsobem
- Zkrátka: všechno, co je potřeba vedět při debuggování CPU, aby z toho bylo poznat, co CPU chce udělat, a ověřit, že to skutečně udělalo - aby šlo jednoduše zkontrolovat, že daná instrukce funguje.
- Toto je povinné, pokud nebude control room v uspokojivém stavu nebo bude úplně chybět, nebudu CPU opravovat!
- Berte to tak, že to děláte i pro sebe - lépe se vám budou hledat chyby a bude si jistější tím, že CPU funguje.
- Této sekci obvodu o velikosti jedné obrazovky říkáme "Control room", a musí v ní být kompaktním a přehledným způsobem vizualizované:
- Vstupy (plusy značí "hodnotu" IO co se týče přivětivosti - pointa je mít něco realistického, použitelného a originálního)
- Sada tlačítek, switchů +
- Joystick ++
- Keyboard +++
- bufferuje znaky, je potřeba klávesnici při přečtení znaku požádat o jeho odstanění z fronty
- Slider ++
- "Magická hodnota od uživatele", tj. input pin
- vhodné např. pokud plánujete ve svém programu provádět výpočty a potřebujete uživatelské číslo
- Sekvenční obvod pro zadávání dat tlačítky, např. keypad na pin apod. ++++
- zde si můžete vymyslet cokoliv a použít jakoukoliv kombinaci vstupních komponent
- Generátor náhodných čísel +
- ...další (ptejte se!)
- Výstupy
- Sada LED +
- LED Bar +
- Sada RGB LED +
- LED matrix ++
- vhodné ukládat aktuální zobrazované data v externích registrech a nechat CPU registry adresovat - jako by tvořily paměť/GPR
- pokud chcete, aby obraz zůstal konstantní mezitím co CPU upravuje registry - druhá řada registrů a "překlopení" dat do nich naráz - tzv. "Double buffering"
- 7-segment displej (s logisimovým BCD-to-7segment +) (s vlastním ++)
- vhodné pokud máte ALU, které umí konverzi na BCD! Jinak můžete zobrazovat hodnoty v hexu...
- Hex displej +
- RGB video +++
- Obsahuje interní framebuffer
- TTY +++
- vypisuje písmena. V kombinaci s klávesnicí tvoří kompletní terminál, na kterém lze implementovat hello world, vlastní shell, etc.
- Buzzer ++ (s timerem +++)
- nastavitelná frekvence a hlasitost
- lze přidat timer, i.e. instrukce zapne buzzer na N clocků (pak se buzzer sám vypne), jednoduchý sekvenční obvod
- stav timeru lze číst v CPU (hodnota a flag zero)
- v kombinaci s klávesnicí lze postavit klávesy, nebo dokonce tracker - e.g. řádek "c7d5e3
" zahraje noty C-D-E na 5-7-3 taktů.
- "Magický output pin" - prefeuji nějaký z displejů
- Alespoň nějaké IO je povinné!
- Blocking vs. nonblocking IO
- Někdy IO operace není připravená, zatím nelze provést, nebo trvá určitý čas. Pak se implementace dělí na (platí i o softwaru):
- e.g. Klávesnice nemá teď žádný znak, který by nám poslala; síťová karta už odesílá něco jiného a je busy, ...
- Blocking - instrukce/funkce/etc. zastaví procesor/thread/etc.
- Je to nutné implementovat, e.g. zastavit procesor dokud nenastane podmínka - ale nesmíme zastavit clock, to nejde.
- Co když po nějaké době už hodnotu nechceme, protože uplynulo moc času? Nejde udělat nic, protože CPU neběží, leda že by mělo nějaky hardwarový timer s timeoutem.
- Většina operací musí být non-blocking - představte si hru, která zamrzne pokaždé, když nic nedržíte, protože čeká na input.
- Non-blocking - instrukce se vždy provede a pokračuje dál, nehledě na úspěch - tzn. může selhat
- V případě selhání (není zmáčknutá klávesa, etc.) má alternativní definované chování - do registru dá nulu / náhodu / nezmění ho.
- Selhání je potřeba oznámit programátorovi! Buď nastavit flag, nebo speciální hodnota (která se nemůže přirozeně vygenerovat) do registru.
- Převést non-blocking na blocking IO je jednoduché - prostě jump zpátky na instrukci, dokud neuspěje!
- Ale můžeme i zkontrolovat jinou podmínku, e.g. čas, a nechat toho a pokračovat v programu
- Non-blocking je v 90% případů užitečnější než blocking!
- Někdy IO operace není připravená, zatím nelze provést, nebo trvá určitý čas. Pak se implementace dělí na (platí i o softwaru):
Jednoduché architektury (ISA)
i8080 / Z80
Architektura mikroprocesoru Intel 8080 je velmi jednoduchá, s syntaxe jejích instrukcí se hodně podobá x86.
Architektura procesor Zilog Z80 je zpětně kompatibilní (naklonovaná) k 8080, ale má další instrukce navíc - tyto rozšíření nebudeme řešit.
- Datová šířka: 8bit, ale některé instrukce umí 16bit
- Šířka instrukce: 8bit + případné immedate operandy (8 nebo 16bit). Operační kód variabilní délky
- Architektura: Akumulátorová
- Registry: A,B,C,D,E,H,L (8bit) a PC,SP (16-bit)
- A je akumulátor
- registry H a L slouží dohromady (High a Low byte) jako 16bit adresa
Mpro práci s datovou pamětí - SP je stack pointer
Popis instrukcí: 8080instructions.pdf
Kódování instrukcí: Tabulka - je zde každá možná varianta každé instrukce v mřížce podle strojového kódu
Programátorská příručka: 8080 Programmers Manual.pdf - 91 stran, obsahuje kompletní informace o ISA. Nečíst, ale otevřít a podívat se na dokumentaci alespoň jedné instrukce, např. instrukcí typu JUMP na straně 37 dokumentu (tj. straně 31 původní knihy).
MIPS I
Verze I architektury MIPS je jednoduchá, ale výkonná ISA. Moderní varianty MIPS naleznete dnes např. v některých routerech, zejména MikroTik.
- Datová šířka: 32bit, novější verze 64bit
- Šířka instrukce: 32bit včetně operandů a 6bit operačního kódu
- Architektura: GPR load-store, 3 operandy
- Registry: $0 až $31, HI, LO (32bit)
- $0 je při čtení vždy 0, a zápisy do něj se ztratí - to zjednodušuje instrukční sadu
- HI, LO jsou speciální registry na specifické operace, e.g. dělení
- Některé registry mají speciální jména a účely, e.g. $29 je $sp (stackpointer)
Popis instrukcí: MIPS_Instruction_Set.pdf
Prezentace o MIPS a o ISA obecně, o programování v assembleru, etc.: mips-isa.pdf
Programátorská příručka: MIPS Programmers Guide - 244 stran, koukněte např. na Computational instructions na straně 50 dokumentu (kapitola 5 strana 10 knihy).
RISC V
Moderní RISC architektura RISC-V vznikla nedávno jako free alternativa k ARM ISA. Konkrétní podoba architektury závisí na zvolených rozšířeních, od mikrokontrolerů (RV32I) až po procesory vhodné na desktop computing (Framework RISC-V mainboard má 4x RV64GCB)
- Datová šířka: 32 nebo 64bit
- Šířka instrukce: 32bit nebo volitelně 16bit
- Architektura: GPR load-store, 3 operandy
- Registry: x0-x31 (32bit)
- Registr x0 je vždy 0
- Některé registry mají speciální názvy a účely
Interaktivní simulátor: comparch.edu.cvut.cz
Cheatsheet instrukcí: RISCV_CARD.pdf
Reference: riscv-unprivileged.pdf - 670 stran, ale pro nás je podstatná pouze kapitola 2 - RV32I Base Integer Instruction Set - to je ~15 stránek velmi hezky formátované a srozumitelné dokumentace k nejdůležitějším instrukcím této ISA.
customasm
Customasm je assembler s nastavitelnou syntaxí instrukcí a kódování strojového kódu.
Doporučuji si přečíst kapitolu customasm wiki, kde se popisuje vytváření přepisovacích pravidel.
Oficiální customasm umí exportovat pouze pro 8-bit a 16-bit Logisim paměti.
Upravená verze (github) umí libovolné 4-32bitové paměti.
Pro nastavení počtu bitů slova instrukce je potřeba na začátek umístit a upravit následující blok, a použít upravenou verzi customasm a použít správný Logisim output formát.
#bankdef code
{
#bits 22
#addr 0x0000
#size 0x8000
#outp 0x0000
}
Pro označení registrů nebo alu operace můžete s výhodou použít #subruledef (skripta, wiki).
Pomocí asm bloku lze realizovat pseudoinstrukce složené z jedné nebo více jiných instrukcí:
ldi {dst: register}, {value: u16} => asm {
xor {dst}, {dst}
addi {dst}, {value[15:8]}
shli {dst}, 8
addi {dst}, {value[7:0]}
}
Užitečné příklady kromě zmíněného můžou být např. skok na immediate adresu (ldi R1 + jmp R1), nop, různé manipulace s flagy.
Stejně jako labely lze použít jako hodnotu (adresu následující instrukce za labelem), lze použít symbol $, který se přeloží na adresu aktuální instrukce (tu customasm zná a dosadí jako číslo). Pomocí tohoto symbolu a výpočtů lze např. realizovat pseudoinstrukci absolutního skoku (na label) pomocí relativního skoku v CPU (více detailů viz advanced rules na wiki):
jmpi {addr: u16} => {
; korekce o -1 nebo podobné bude záviset na tom,
; jak vaše CPU interpretuje relativní adresy
reladdr = addr - $ - 1
asm { jmpri {reladdr} }
}
Generování zobrazovacích instrukcí pro 16x16 LED matrix displej
Studenti Maxim Sklenář a Joshua Remington v roce 2025 vytvořili webovou aplikaci, pomocí které lze generovat instrukční posloupnost, která zobrazí zadaný pixelart na 16x16 LED matrix displeji.
Markdown
Tyto skripta se kompilují pomocí mdbook, je tedy možné používat všechny tímto programem podporované konstrukce.
Časem je cílem podorovat i build do pdf, což nejspíš omezí některé syntaxe, aby mohl proběhnout build do html i do pdf ze stejného zdrojového kódu.
Navíc jsou do mdbook nainstalované preprocessory, které umožňují používat další druhy syntaxe. Preprocesory jsou uvedeny cca v pořadí, ve kterém se spoštějí:
checklist 📘
Umožňuje vložit do markdownu inline TODO, ze kterých se udělá globální seznam ve speciální kapitole, s odkazy.
Příklad
Kvůli konfliktu syntaxu s jinja templatováním je nutné použít pro vytvoření TODO jinja makro:
{{ todo("This and that needs to be done") }}
minijinja 📘
Umožňuje napříč celými skripty používat jinja templates (specifikace) pomocí implementace minijinja (rozdíly oproti specifikaci).
Templates, včetně souborů obsahující makra, jsou ve složce templates. Globální proměnné lze přidat v book.toml.
Naimportování všech důležitých maker lze provést pomocí {% include prelude %}, kde prelude je v book.toml zadefinované jako "prelude.md", které se nachází v templates/ a importuje makra. NEW: prelude se includuje ve všech kapitolách automaticky, není potřeba includovat nic z ní.
Příklad
{% set authors = ["Michal Vojáček", "Michal Javor"] %}
Autoři těchto skript jsou {{ authors | join(", ") }}.
| Číslo | Autor |
|------:|:------|
{% for author in authors -%}
| {{ loop.index }} | {{ author }} |
{% endfor -%}
| end | end |
{% call spoiler(el="div") %}
{{ gate("xor", "OUT", "IN1", "IN2") }}
{% endcall %}
Autoři těchto skript jsou Michal Vojáček, Michal Javor.
| Číslo | Autor |
|---|---|
| 1 | Michal Vojáček |
| 2 | Michal Javor |
| end | end |
cmdrun 📘
Umožňuje do skript přidat výstup libovolného unix příkazu, což je užitečné např. pro generování výstupů z logisimu, nebo buildování latexu.
Přichází s tím samozřejmě určitý risk, proto doporučuji provozovat mdbook builder v dockeru. Všechny použití tohoto preprocesoru lze najít pomocí:
grep -roP '\<\!\-\- cmdrun\K.+(?=\-\-\>)' --exclude-dir book .
Příklad
Jako příklad seznam všech použití toho preprocesoru ve skriptech (příkaz výše):
./src/90_ostatni/markdown.md: cd ../.. && grep --color=no -roP '\<\!\-\- cmdrun\K.+(?=\-\-\>)' --exclude-dir book .
katex 📘
Umožňuje použití $ a $$ pro psaní matematických výrazů.
Příklad
image-size 📘
Markdown neumožňuje specifikaci velikosti a centrování obrázků, tento preprocesor tuto funkcionalitu přidává.
Do budoucna chci projekt upravit a rozvolnit syntaxi, aby šlo specifikovat pouze zarovnání, bez šířky.
✏️ TODO: Forknout mdbook-image-size a rozvolnit syntaxi
Příklad

admonish 📘
Umožňuje vytvářet HTML "bannery", které volitelně můžou být rozbalovací.
Vyvolává se pomocí ```admonish info title="Title",collapsible=true, kde místo info můžou být následující vestavěné styly:
Příklad
quiz
toc
kroki
emojicodes 📘
Umožňuje vkládat do textu emoji pomocí Github shortcode ohraničeného ::
Příklad
👨❤️👨 👩❤️👩 ✅ 🏳️🌈 🏳️⚧️
embedify
footnote
pagetoc 📘
Přidává na generovanou stránku vpravo sidebar s navigací v aktuální kapitole, pokud na nej je horizontální místo ve viewportu.
Poděkování
Děkuji všem zmíněným za pomoc při tvorbě skript
- @jaywor1 - řešitel maturitního projektu 2023/24, ve kterém vznikla prvotní verze skript
- GitHub - https://github.com/jaywor1
- @aestheticdisaster - pomoc s pravopisem během maturitního projektu
- GitHub - https://github.com/aestheticdisaster
- @mvojacek - oponent maturitního projektu, učitel APS a současný správce skript
- GitHub - https://github.com/mvojacek
Zdroje
Čitelný formát
Wikipedia
- https://cs.wikipedia.org/wiki/Karnaughova_mapa
- https://cs.wikipedia.org/wiki/Adresní_sběrnice
- https://en.wikipedia.org/wiki/Control_bus
Obrázky
- https://commons.wikimedia.org/wiki/File:Buffer_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:NOT_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:AND_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:OR_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:NAND_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:NOR_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:XOR_ANSI_Labelled.svg
- https://en.wikipedia.org/wiki/File:XNOR_ANSI_Labelled.svg
- https://commons.wikimedia.org/wiki/File:K-map_minterms_A.svg
- https://commons.wikimedia.org/wiki/File:SR_Flip-flop_Diagram.svg
- https://commons.wikimedia.org/wiki/File:D-type_Transparent_Latch_(NOR).svg
- https://commons.wikimedia.org/wiki/File:Edge_triggered_D_flip_flop.svg
- https://commons.wikimedia.org/wiki/File:Edge_triggered_D_flip_flop_with_set_and_reset.svg
- https://commons.wikimedia.org/wiki/File:Negative-edge_triggered_master_slave_D_flip-flop.svg
- https://commons.wikimedia.org/wiki/File:D-Type_Flip-flop_Diagram.svg
- https://commons.wikimedia.org/wiki/File:4_Bit_Shift_Register_001.svg
- https://commons.wikimedia.org/wiki/File:Harvard_architecture.svg
- https://commons.wikimedia.org/wiki/File:Von_Neumann_Architecture.svg
- https://commons.wikimedia.org/wiki/File:ABasicComputer.svg
Gify
Tex
ČSN ISO 690
[1] RUST-LANG, nedatováno. Rust-Lang/mdbook: Create book from markdown files. like Gitbook but implemented in rust. GitHub [online] [vid. 25. únor 2024]. Získáno z: https://github.com/rust-lang/mdBook
[2] ANON., 2022a. Karnaughova Mapa. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://cs.wikipedia.org/wiki/Karnaughova_mapa
[3] ANON., 2022a. Adresní SBĚRNICE. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://cs.wikipedia.org/wiki/Adresn%C3%AD_sb%C4%9Brnice
[4] ANON., 2023. Control Bus. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://en.wikipedia.org/wiki/Control_bus
[5] ANON., nedatováno. Example: Visualisation of two’s complement for a 4-bit-value. TeXample.net [online] [vid. 25. únor 2024]. Získáno z: https://texample.net/tikz/examples/complement/
[6] ANON., 2024. Karnaugh map. Wikipedia [online] [vid. 25. únor 2024]. Získáno z: https://en.wikipedia.org/wiki/Karnaugh_map#/media/File:Torus_from_rectangle.gif
[7] ANON., nedatováno. File:Buffer ANSI Labelled.svg. Wikimedia Commons [online] [vid. 25. únor 2024 b]. Získáno z: https://commons.wikimedia.org/wiki/File:Buffer_ANSI_Labelled.svg
[8] File:NOT ANSI labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:NOT_ANSI_Labelled.svg
[9] ANON., nedatováno. File:Buffer ANSI Labelled.svg. Wikimedia Commons [online] [vid. 28. únor 2024 b]. Získáno z: https://commons.wikimedia.org/wiki/File:Buffer_ANSI_Labelled.svg
[10] File:or ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:OR_ANSI_Labelled.svg
[11] File:NAND ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:NAND_ANSI_Labelled.svg
[12] File:nor ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:NOR_ANSI_Labelled.svg
[13] File:XOR ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:XOR_ANSI_Labelled.svg
[14] File:XNOR ANSI Labelled.svg. Wikimedia Commons [online]. [vid. 27. únor 2024]. Získáno z: https://commons.wikimedia.org/wiki/File:XNOR_ANSI_Labelled.svg
[15] ANON., nedatováno. File:K-map minterms a.svg. Wikimedia Commons [online] [vid. 28. únor 2024 d]. Získáno z: https://commons.wikimedia.org/wiki/File:K-map_minterms_A.svg
[16] ANON., nedatováno. File:Sr Flip-flop diagram.svg. Wikimedia Commons [online] [vid. 28. únor 2024 e]. Získáno z: https://commons.wikimedia.org/wiki/File:SR_Flip-flop_Diagram.svg
[17] ANON., nedatováno. File:d-type transparent latch (NOR).SVG. Wikimedia Commons [online] [vid. 28. únor 2024 d]. Získáno z: https://commons.wikimedia.org/wiki/File:D-type_Transparent_Latch_(NOR).svg
[18] ANON., nedatováno. File:edge triggered D flip flop.svg. Wikimedia Commons [online] [vid. 29. únor 2024 e]. Získáno z: https://commons.wikimedia.org/wiki/File:Edge_triggered_D_flip_flop.svg
[19] ANON., nedatováno. File:edge triggered D flip flop with set and reset.svg. Wikimedia Commons [online] [vid. 29. únor 2024 e]. Získáno z: https://commons.wikimedia.org/wiki/File:Edge_triggered_D_flip_flop_with_set_and_reset.svg
[20] ANON., nedatováno. File:negative-edge triggered master slave D flip-flop.svg. Wikimedia Commons [online] [vid. 29. únor 2024 h]. Získáno z: https://commons.wikimedia.org/wiki/File:Negative-edge_triggered_master_slave_D_flip-flop.svg
[21] ANON., nedatováno. File:D-type flip-flop diagram.svg. Wikimedia Commons [online] [vid. 29. únor 2024 d]. Získáno z: https://commons.wikimedia.org/wiki/File:D-Type_Flip-flop_Diagram.svg
[22] ANON., nedatováno. File:4 bit shift register 001.SVG. Wikimedia Commons [online] [vid. 29. únor 2024 b]. Získáno z: https://commons.wikimedia.org/wiki/File:4_Bit_Shift_Register_001.svg
[23] ANON., nedatováno. File:Harvard architecture.svg. Wikimedia Commons [online] [vid. 29. únor 2024 i]. Získáno z: https://commons.wikimedia.org/wiki/File:Harvard_architecture.svg
[24] ANON., nedatováno. File:von Neumann Architecture.svg. Wikimedia Commons [online] [vid. 29. únor 2024 m]. Získáno z: https://commons.wikimedia.org/wiki/File:Von_Neumann_Architecture.svg
[25] ANON., nedatováno. File:abasiccomputer.svg. Wikimedia Commons [online] [vid. 29. únor 2024 c]. Získáno z: https://commons.wikimedia.org/wiki/File:ABasicComputer.svg
Checklist
-
Logická hradla:
- zbytek stranky (TODO)
-
Booleova algebra:
- Přepsat stránku (TODO)
-
Karnaughova mapa:
- Přepsat stránku (TODO)
-
Příprava na test:
- druhý test (TODO)
-
Základy:
- Přepsat stránku (TODO)
-
Třetí stav a zkraty:
- Přepsat stránku (TODO)
-
Multiplexory a dekodéry:
- Přepsat cvičení (TODO)
-
Komparátor:
- Přepsat stránku (TODO)
-
Sekvenční obvody:
- Přepsat stránku (TODO)
-
Asynchronní obvody:
- Přepsat stránku (TODO)
-
Synchronní obvody:
- Přepsat stránku (TODO)
-
Úvod:
- Přepsat stránku (TODO)
-
Návrh:
- Přepsat stránku (TODO)
-
Stavba:
- Přepsat stránku (TODO)
-
Programování:
- Přepsat stránku (TODO)
-
Markdown:
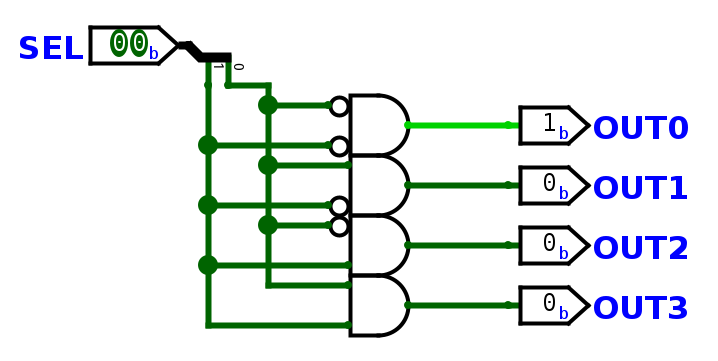
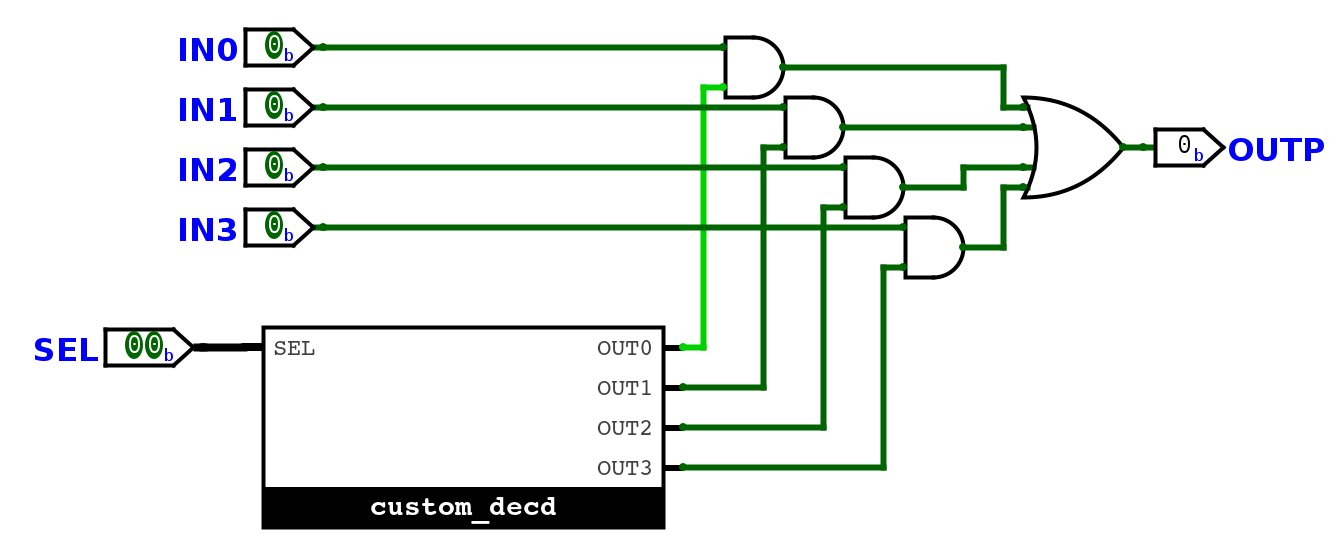
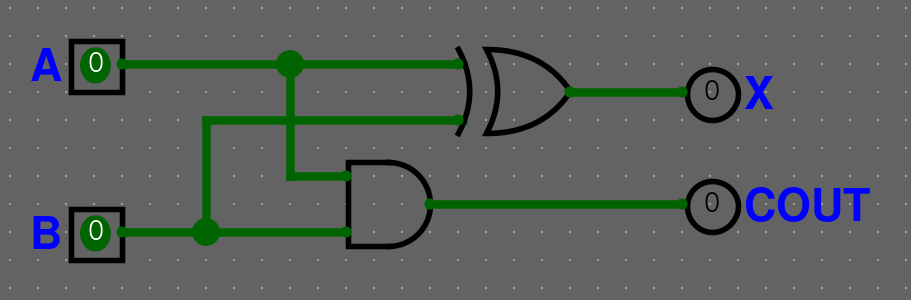
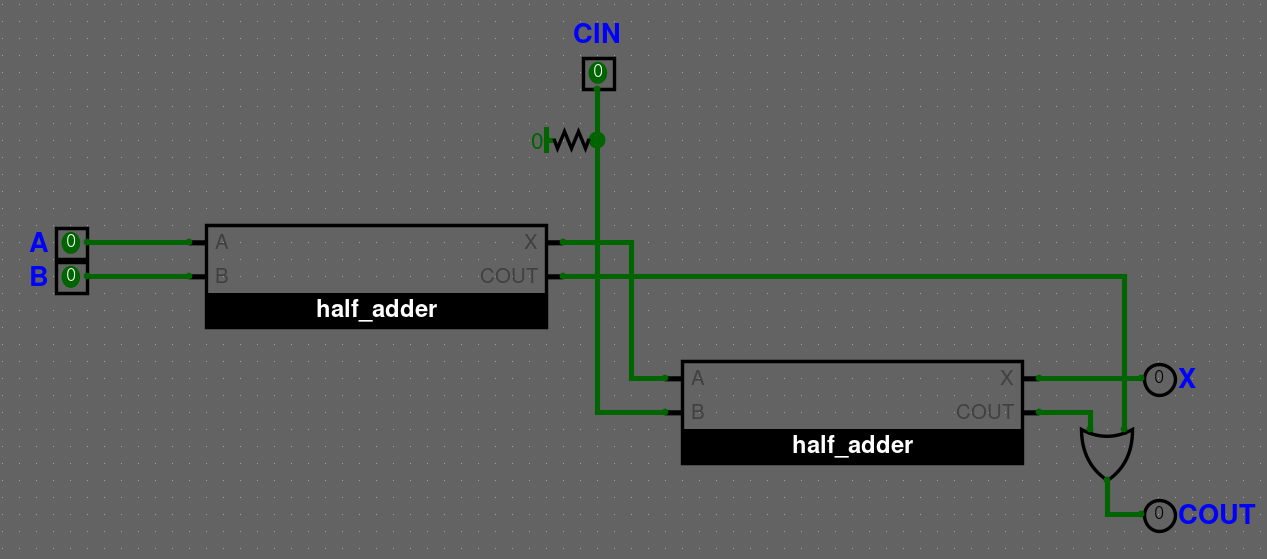
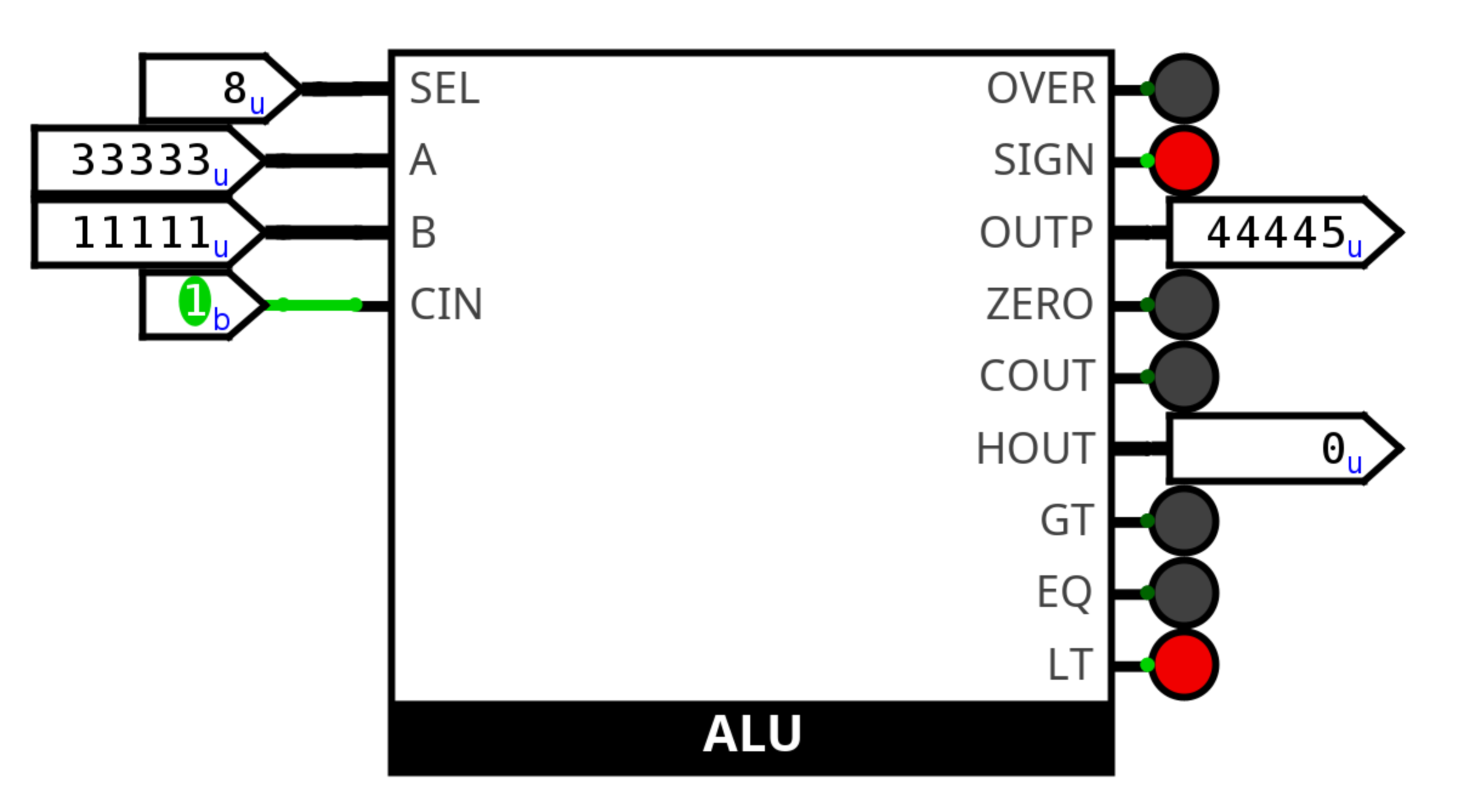
.svg.png)