Zadání projektu ALU

Vytvořte v Logisim Evolution modul tzv. Aritmeticko-Logické jednotky (ALU). ALU je (v našem provedení) kombinační obvod, který umí provést vždy jednu vybranou z několika podporovaných aritmetických nebo logických operací.

Formální náležitosti odevzdání

Danger

V případě nedodržení některého z těchto požadavků bude ALU hodnoceno 0 body.

Odevzdání

Odevzdávání probíhá na platformě Submitty hostované mnou na adrese: https://submit.vojacek.org. Pro přihlášení potřebujete přihlašovací údaje, které jste dostali automatizovaným emailem (zkuste se podívat i do spamu, a email ze spamu přesuňte do doručených, aby se vám nesmazal!). Více informací naleznete právě v tomto emailu. V případě problémů mě kontaktujte emailem.

V případě, že by systém nefungoval, je záložní metoda odevzdání emailem. V takovém případě odevzdáváte vždy přímo v příloze zip archiv pojmenovaný alu_{jmeno}_{prijmeni}_{cislo odevzdani}.zip. Odkazy na OneDrive atp. nejsou přípustné, protože jejich obsah lze upravit po odevzdání. Projekt ALU se bez problému vejde přímo do emailu.

Soubory odevzdání

Název souboru	Popis
ALU.circ	Projektový soubor Logisimu obsahující ALU
*.circ	Libovolné další .circ soubory nutné pro funkčnost ALU
OPCODES.txt	Strojově čitelný popis operačních kódů implementovaných v ALU
Dokumentace.xlsx/.ods	Uživatelsky přívětivá dokumentace ALU
README.md	Jakékoliv další připomínky k odevzdání

Warning

Je potřeba dodržet přesné názvy souborů, včetně kapitalizace! ALU budu vyhodnocovat částečně strojově, v případě špatně pojmenovaných souborů nepůjde ohodnotit.

Projekt v Logisimu

Použijte Logisim Evolution 3.9.0
Modul ALU v Logisimu se musí jmenovat ALU. Pokud ho máte jiný, vytvořte správně pojmenovaný modul a překopírujte obsah (Ctrl-A, Ctrl-C, Ctrl-V).
Všechna dvou-vstupová hradla musí mít velikost Narrow, pokud není vyloženě vhodné mít jinou. Doporučuji použít template.
Všechny moduly mají pojmenované všechny vstupy a výstupy vhodným jménem.
Používání třetího stavu (a jej generující komponenty) je obecně zakázáno. U každého použití je nutné odůvodnit (text toolem v logisimu v místě použití), proč je to vhodné místo klasických hradel a že nenastává žádný z problémů obecně spojeným s třetím stavem.
V ALU je dovoleno je používat následující komponenty z knihoven:
- Wiring: Splitter, Pin, Probe, Tunnel, Constant
- Gates: NOT, Buffer, AND, OR, NAND, NOR, XOR, XNOR
Pro postavení modulu ALU by neměly být žádné jiné komponenty potřeba. V případě nejasností se ptejte. Mimo modul ALU můžete použít libovolné komponenty - např. pro testování, ukázku, etc.
V ALU je pouze jedna instance 16-bit sčítačky. Všechny operace, které ji potřebují, se na ní musí vystřídat, ALU provádí pouze jednu operaci zároveň. Použití více sčítaček je penalizováno jako hrubá neefektivita zapojení.

Bonusové operace

Pro implementování bonusových operací jsou tyto restrikce rozvolněné. Např. uvnitř násobičky můžete použít vestavěnou sčítačku, čímž se zásadně zrychlí simulace obvodu. Dokonce to doporučuji. Nemůžete ale např. pro implementaci násobičky použít logisimovou násobičku.

V modulu main, alu_main, alu_showcase nebo podobně bude implementovaná showcase vašeho ALU:
- Je zde položený váš ALU modul
- Všechny vstupy jsou odvozené z komponent, kterým lze jednoduše upravovat hodnota v decimal nebo hexadecimal (např. input pin se správně nastaveným radixem)
- Všechny výstupy jsou napojené na komponenty, na kterých je srozumitelně vidět jejich hodnota (opět decimal nebo hexadecimal) (např. LED, output pin se správně nastaveným radixem)
- Radix (soustava, e.g. decimal nebo hexadecimal) všech vstupů a výstupů je stejný

Příklad showcase

Dokumentace.xlsx

Každý číslicový modul (v praxi se používá zkratka IP znamenající Intellectual Property) musí mít detailní dokumentaci, často jsou to dokumenty o desítkách až stovkách stran.

Interní dokumentace slouží pro zorientování v implementaci modulu a navázání na vývoj po delší době nebo po kolegovi. Tu u ALU vynecháme.

Externí dokumentace dokumentuje interface (vstupy a výstupy) modulu, jeho operační režimy, chování, zakázané kombinace vstupů, případně elektrické vlastnosti. U nás jako 90% externí dokumentace slouží toto zadání - vstupy, výstupy a chování jsou tu přesně popsané. Je ale potřeba zdokumentovat hodnoty vstupu SEL, které jsou plně ve vaší režii.

Pro tento účel jako součást odevzdání ALU vypracujete soubor Dokumentace.xlsx (nebo .ods), ve kterém tohle chování popíšete. Formát a obsah dokumentace není striktně definovaný, ale měl by pro každou implementovanou operaci obsahovat v přehledné podobě alespoň následující informace:

Hodnotu SEL v desítkové soustavě (jako v OPCODES.txt)
Binární rozvoj SEL s obravenými buňkami. Bity uspořádejte tak, že MSB bude vlevo.
ID operace
Mnemoniku krátce vystihující chování operace (příklady máte uvedené ve sloupci Mnemo v tabulkách a v obrázku níže. Není tu správná a špatná odpověď, stačí si vymyslet krátký "assemblerový" způsob, kterým by mohl programátor tuto operaci chtít použít v programu. Důležité je pouze, aby vámi zvolený styl byl konzistentní napříč celou ALU dokumentací)
Stručný slovní popis operace (e.g. Sečte A, B a CIN. Výsledek je OUTP, COUT. Spočítá OVER, ZERO, SIGN.)

Podmíněné formátování

Pro automatické podbarvení buněk s binárním rozvojem můžete použít podmíněné formátování. Na použítých stylech nezáleží, stačí, aby byly odlišné.

Tyto údaje má smysl formátovat do tabulky (proto xlsx), a takové tabulce nesmí chybět hlavička. Obzvlášť u binárního rozvoje je vhodné označít číslo každého bitu, případně MSB a LSB (Most- a Least-Significant-Bit).

Příklad dokumentace:

OPCODES.txt

Soubor OPCODES.txt je strojově čítelnou verzí dokumentace, která slouží pro automatizovaný opravovač, aby věděl, jaké operace jste implementovali a jak je nechat ALU spočítat. Je to CSV bez hlavičky s řádky ve formátu {opcode},{ID}, např.

0,and
1,or
2,not
3,cla
15,mul8

opcode je zde číslo, které se přívádí na vstup SEL, zapsané v desítkové soustavě. "opcode" je zkratka pro operation code, neboli číslo identifikující operaci.

ID je ID operace, jak je uvedené ve sloupci ID v tomto zadání, nebo custom jako označení oprace, která není v zadání (pro vyjímečné případy, kdy chcete naimplementovat nějakou jinou operaci navíc za bonusové body).

Info

V případě použití custom budu danou operaci hodnotit ručně, je tedy potřeba, aby byla detailně popsaná v dokumentaci ALU.

Na pořadí nezáleží, a v souboru nesmí být žádné jiné údaje. Sada popsaných operací musí být konzistentní s dokumentací!

Plagiáty

Všechny projekty v předmětu APS jsou samostatné práce, musí tedy produktem vaší vlastní práce. Je povoleno projekty probírat, konzultovat, nechat si pomoct s řešením problému. Je nepřípustné odevzdávat cizí práci, a to včetně případů, kdy jste obvod podle předlohy zapojili sami.

Ve skriptech a na internetu je dostatek informací pro řešení projektu, je nutné danou problematiku pochopit.

Do výsledného hodnocení se bude vždy započítávat pouze vaše vlastní práce. V případě porušení budou uděleny nevratné záporné body.

Hodnocení

Za ALU, které správně implementuje všechny zadané operace, je možné získat až 20 bodů.

V případě, že povinné ALU je hodnocené 20 body, je možné získat až 6 bonusových bodů za bonusové operace.

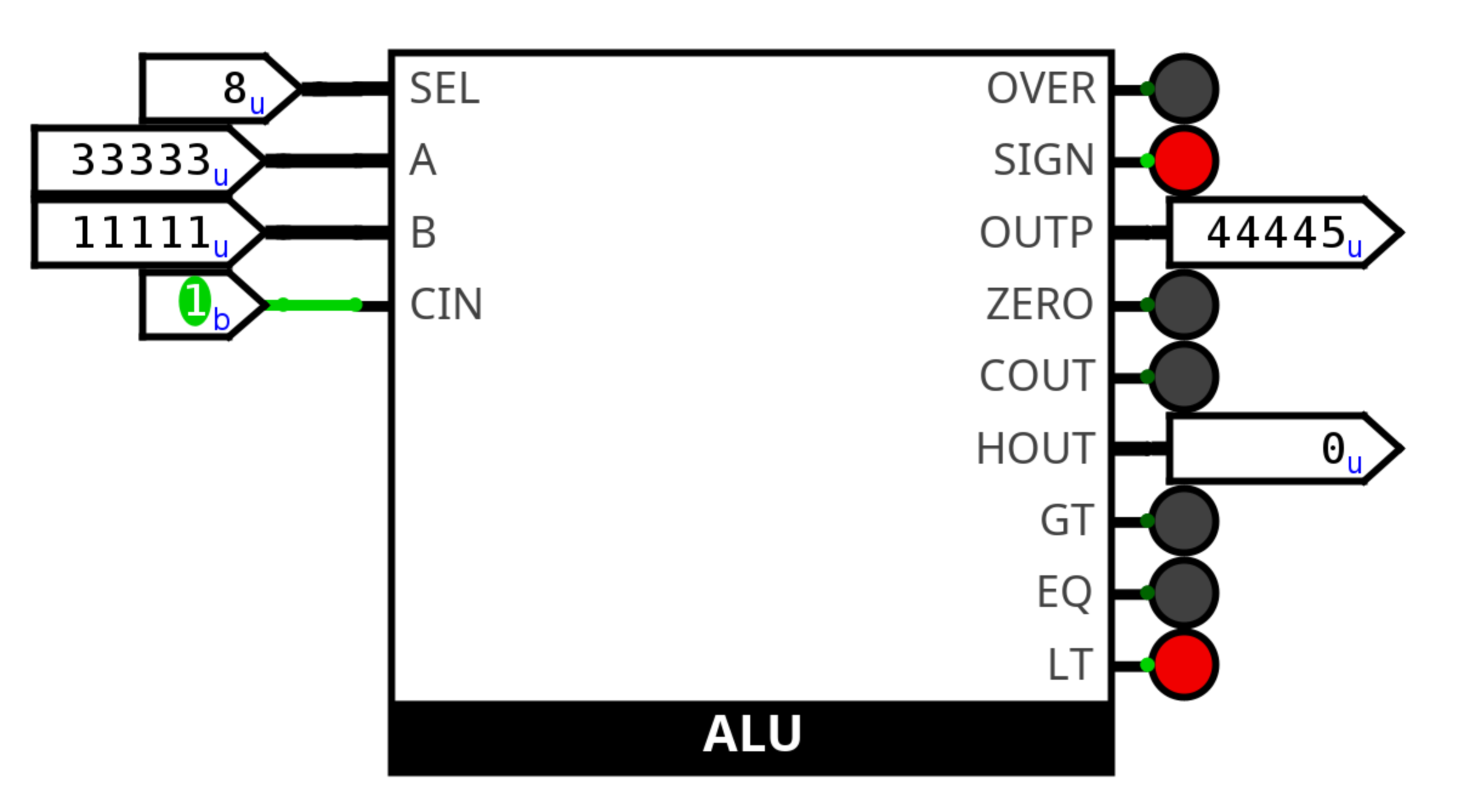
Vstupy a výstupy (I/O) ALU

Naše ALU je 16-bitové, to znamená že umí zpracovat data (čísla) o šířce 16 bitů. Z toho vyplývá, že všechny vstupy a výstupy, kterými tečou data (čísla), musí mít 16 bitů.

Název v Logisimu	I/O	Šířka	Popis funkce
`A`, `B`	IN	16	16-bitové vstupy do ALU
`CIN`	IN	1	Vstup carry-in (borrow-in) pro některé ALU operace (+, -, posuny, ...)
`SEL`	IN	4	Vybírá aktuálně prováděnou operaci v ALU
`OUTP`	OUT	16	16-bitový výstup z ALU
`HOUT`	OUT	16	Horní polovina výsledku, pokud je výsledek operace širší než 16 bitů (např. násobení 16bit x 16bit)
`COUT`	OUT	1	Výstup carry-out (borrow-out) pro některé ALU operace (+, -, posuny, ...)
`ZERO`	OUT	1	Indikuje, že `OUTP` je roven `0`
`SIGN`	OUT	1	Indikuje, že `OUTP`, pokud ho interpretujeme ve dvojkovém doplňku, je záporné číslo
`OVER`	OUT	1	V případě, že došlo k součtu, indikuje, že pokud by se operace brala jako ve dvojkovém doplňku, je výsledek nevalidní (nevešel se do reprezentovatelného rozsahu)
`GT`, `LT`, `EQ`	OUT	1	Indikují vztah porovnání mezi `A` a `B` nezávisle na aktuálně vybrané operaci. `GT` se rozumí `A > B`.

Info

Ne všechny I/O musí být nutně přítomné, pouze ty, které jsou potřeba pro nějakou z implementovaných operací. Taky je přípustné mít I/O navíc, které slouží nějaké funkcionalitě nad rámec, nebo bonusovým operacím - v takových situacích bude funkcionalita ověřena ručně.

Important

Vstupy a výstupy musí být pojmenované přesně podle tabulky, jinak jejich hodnota nebude při opravování brána v potaz! Modul ALU se musí jmenovat ALU!

Definovanost výstupů a relevance vstupů

Následující tabulka definuje, které výstupy musí být pro danou operaci smysluplně definované (mít hodnotu podle definice operace) a na kterých vstupech hodnota závisí.

Hint

Jako rule of thumb platí: každý výstup z ALU by měl být vypočten pomocí aktuálně vybrané operace v ALU, nebo být $0$ pokud to nedává smysl.

ID	Inputy	Outputy
`xor`, `or`, `and`	$A, B$	$OUTP$
`not`	$A$	$OUTP$
`shr`, `shl`	$A, CIN$	$OUTP, COUT$
`rotr`, `rotl`	$A$	$OUTP$
`add`	$A, B, CIN$	$OUTP, COUT, OVER$
`sub_half`	$A, B$	$OUTP, OVER$
`sub_full`	$A, B, CIN$	$OUTP, COUT, OVER$
`inc`	$A$	$OUTP, COUT, OVER$
`dec`	$A$	$OUTP, OVER$
`mul8`	$A_{[7:0]}, B_{[7:0]}$	$OUTP$
`mul16`	$A, B$	$HOUT, OUTP$
`swap8`	$A$	$OUTP$
`bsh`	$A, B_{[3:0]}, CIN$	$OUTP$
`bshl`	$A, B_{[3:0]}$	$OUTP$
`bshr`	$A, B_{[3:0]}$	$OUTP$
všechny		$ZERO, SIGN$
binární		$GT, LT, EQ$

Note

V ostatních případech musí hodnota těchto výstupů být $0$ ! Není přípustné, aby na výstupech kdykoliv byl třetí stav, error, nebo náhodná/nerelvantní hodnota.

Operace ALU

Pseudokód

$A \leftarrow B$ značí assignment, tedy že bity z B se použijí pro konstrukci A (výsledku).

${A, B}$ značí konkatenaci, tedy že bity A a B se spojí do širší hodnoty, více důležité bity vlevo. Do takové hodnoty lze i assignovat.

$\forall i$ v tomto kontextu značí "pro všechny $i$ (indexy bitů)", kromě indexů, pro které operaci nelze provést. Typicky 0..15, což jsou indexy bitů 16-bitové hodnoty, kde index $0$ je LSB (Least Significant Bit).

$A_{[7:0]}$ značí slice neboli bitový výběr. V tomto případě vybereme bity 7 až 0, ve výsledné hodnotě budou uspořádané tak, že bit z je nejvíc vlevo (MSB), tedy neměníme pořadí bitů.

Typy operací

Typ	Význam
‼️	Povinné a důležité
❗	Povinné
❓	...za určitých podmínek
🤷‍♂️	Volitelné
🧑‍🎓	Bonusové

Operace po bitech (bitwise)

Typ	ID	Mnemo	Pseudokód	Popis
‼️	`xor`	A XOR B	$\forall i : OUTP_{i} \leftarrow A_{i} \oplus B_{i}$	XOR A a B po bitech
‼️	`or`	A OR B	$\forall i : OUTP_{i} \leftarrow A_{i} + B_{i}$	OR A a B po bitech
‼️	`and`	A AND B	$\forall i : OUTP_{i} \leftarrow A_{i} \cdot B_{i}$	AND A a B po bitech
‼️	`not`	NOT A	$\forall i : OUTP_{i} \leftarrow \overline{A_{i}}$	NOT A po bitech

Více informací na wikipedii: Bitwise operators

Posuny a rotace (shifts and rotations)

Typ	ID	Mnemo	Pseudokód	Popis
‼️	`shr`	SHR A	$\forall i : OUTP_{i} \leftarrow A_{i + 1}$ $OUTP_{15} \leftarrow CIN$ $COUT \leftarrow A_{0}$	Logický posun doprava
‼️	`shl`	SHL A	$\forall i : OUTP_{i} \leftarrow A_{i - 1}$ $OUTP_{0} \leftarrow CIN$ $COUT \leftarrow A_{15}$	Logický posun doleva
‼️	`rotr`	ROTR A	$\forall i : OUTP_{i} \leftarrow A_{i + 1}$ $OUTP_{15} \leftarrow A_{0}$	Rotace doprava
‼️	`rotl`	ROTL A	$\forall i : OUTP_{i} \leftarrow A_{i - 1}$ $OUTP_{0} \leftarrow A_{15}$	Rotace doleva

Tip

Pomocí logických posunů (a správného použití carry) lze rychle provést dělení a násobení dvěma, a to jak u čísel bez znaménka, tak u čísel v doplňkovém kódu.

Shifty

Info

Takto naspecifikovaný logický posun se někdy nazývá rotace skrz carry.

Shift left (rotate left through carry)

Shift right (rotate right through carry)

Více informací na wikipedii: Rotate through carry

Rotace

Rotate left

Rotate right

Vice informací na wikipedii: Rotate

Sčítání a odčítání

Typ	ID	Mnemo	Pseudokód	Popis
‼️	`add`	A ADD B	${COUT, OUTP}$ $\leftarrow A + B + CIN$	Součet respektující carry
‼️ ❓	`sub_half`	A SUB B	$OUTP \leftarrow A - B$	Rozdíl bez borrow
‼️ ❓	`sub_full`	A SUB B	${COUT, OUTP}$ $\leftarrow A - B - CIN$	Rozdíl respektující borrow
❗	`inc`	INC A	${COUT, OUTP}$ $\leftarrow A + 1$	Zvětšení A o 1
❗	`dec`	DEC A	$OUTP \leftarrow A - 1$	Změnšení A o 1

Info

Z operací sub_half a sub_full stačí implementovat pouze jednu. V případě volby sub_half bude pomocí ALU obtížné odečítat větší než 16bit hodnoty.

Warning

Operace inc a dec neberou v potaz hodnotu CIN a provádějí vždy úpravu o 1!

Operace inc musí správně vygenerovat COUT!

Operace dec nemusí správně vygenerovat COUT (netestuje se).

Operace add, sub_half, sub_full, inc, dec musí generovat OVER, pro případ, že jim programátor dal čísla se znaménkem.

Jedna sčítačka

Pro implementaci všech 4 "sčítacích" operací je potřeba použít pouze jedinou sčítačku. Protože ALU vždy vykonává pouze jednu vybranou operaci, jedna instance sčítačky stačí, a jednolivé operace se na ní musí "vystřídat".

Více informací v kapitolách o sčítání a odčítání.

Bonusové

Info

Pro všechny bonusové operace platí, že můžete používat libovolné komponenty, kromě těch, které přímo implementují danou operaci.

Např. v mul můžete použít jakoukoliv sčítačku, ale ne (vestavěnou) násobičku. V cla nesmíte použít vestavěnout sčítačku. V barrel shifteru nesmíte použít jakýkoliv vestavěný shifter. etc.

Typ	ID	Mnemo	Pseudokód	Popis
🧑‍🎓	`mul16`	A MUL B	${HOUT, OUTP}$ $\leftarrow A * B$	16bit násobení A a B
🧑‍🎓 ❓	`mul8`	AL MUL BL	$OUTP$ $\leftarrow A_{[7:0]} * B_{[7:0]}$	8bit násobení spodních polovin A a B
❗ ❓	`swap8`	SWAP8 A	${A_{[15:8]}, A_{[7:0]}}$ $\leftarrow {A_{[7:0]}, A_{[15:8]}}$	Výměna horního a spodního bytu A
🧑‍🎓	`mul16k`	A MUL B	viz `mul16`	16b násobení pomocí Karatsubova alg.
🧑‍🎓	`cla`	A ADD B	viz `add`	Použijte místo `add` pokud jste implementovali CLA.
🧑‍🎓	`bsh`	A SHC B	$i f CIN$ $A \leftarrow A << B_{[3:0]}$ $e l se$ $A \leftarrow A >> B_{[3:0]}$	Posun A o B doleva/doprava
🧑‍🎓 ❓	`bshl`	A SHL B	$A \leftarrow A << B_{[3:0]}$	Posun A o B doleva
🧑‍🎓 ❓	`bshr`	A SHR B	$A \leftarrow A >> B_{[3:0]}$	Posun A o B doprava
🧑‍🎓	`bcd`	BCD A	-	převod A na BCD

Násobení (~2b)

Stačí implementovat násobičku kladných čísel podle naivního násobení pod sebou. Za pokročilejší řešení (násobení čísel ve dvojkovém doplňku, efektivnější násobička jako Dadda nebo Wallace multiplier) získáte větší počet bodů (indikujte v README).

Varianty

Pro splnění násobení je potřeba implementovat buď mul16 (velká operace), nebo mul8+swap8 (menší operace + pomocná operace). V obou případech bude možné násobit libovolně velké čísla v softwaru pomocí částečných násobků.

Doporučuji variantu mul8+swap8, protože bude v obvodu mnohem méně hradel, což urychlí simulaci.

V případě implementace barrel shifteru lze operaci swap8 vynechat, protože jí lze nahradit pomocí série operací bshl, bshr, or.

Alternativně lze za více bodů rozšířit mul8 na mul16 pomocí Karatsubova algoritmu (viz níže).

Doporučení

Používejte během stavění moduly, pokud potřebujete opakovat nějakou část obvodu.

Karatsubovo efektivní násobení (~1b navíc k násobení)

Alternativní způsob implementace 16bit násobení, pokud už máte postavenou 8bit násobičku.

Standardně je pro implementaci 16bit násobení potřeba provést čtyři 8bit násobky (AL*BL, AL*BH, AH*BL, AH*BH) a posčítat správně výsledky. To odpovídá klasickému "naivnímu" školnímu násobení pod sebou.

Ovšem Anatolij Alexejevič Karacuba (anglicky Karatsuba) v roce 1962 publikoval algoritmus, pomocí kterého lze 16bit násobení provést pouze pomocí tří 8bit násobků, za cenu několika sčítání navíc.

Tento Karatsubův algoritmus se hodí primárně pro urychlení velkých násobků v softwarových rutinách, kde máme od hardwaru k dispozici pouze 8b/16/32b násobení. Počet hardwarových násobení, které je potřeba provést pro vypočtení nbit x nbit násobku je $O (n^{l o g_{2} 3}) \approx O (n^{1.58})$ , což je podstatný rozdíl oproti naivnímu násobení pod sebou, kde je to $O (n^{2})$ .

Pro implementaci v HW se hodí spíše násobičky založené na efektivnější redukci součtů (Dadda, Wallace), nicméně pro porozumění algoritmu poslouží i jeho implementace v HW.

Zadání

Buď:

implementujte 8bit násbičku klasicky, nebo
implementujte 4bit násobičku klasicky, a pomocí tří jejich instancí dle Karatsubova algoritmu zapojte 8bit násobičku.

Poté, pomocí tří 8bit násobiček dle Karatsubova algoritmu zapojte 16bit násobičku. Touto násobičkou implementujte operaci mul16, ale označte ji v OPCODES.txt jako mul16k.

Sčítačka s predikcí přenosů (CLA) (~2b)

Neboli Carry Lookahead Adder (CLA). Klasický postup sčítání zprava doleva (Ripple-carry adder) je pomalý. Analýzou vztahu carry-in jednotlivých full-adderů ke vstupům lze zjistit, že každý carry-in/out lze předpovědět přímo ze předchozích vstupů vypočtením několika násobků, které se sečtou. Tedy čas pro výpočet bude vždy pouze daný pouze rychlostí vícevstupového AND (kterých se provede několik paralelně) a následného vícevstupového OR. Při implementaci v tranzistorech je vícevstupový AND/OR rychlejší, než řetězec hradel XOR+OR, který najdeme v klasickém ripple-carry adderu (RCA).

Získáváme tedy recept na to, jak postavit sčítačku, kde rychlost výpočtu výsledku je kvazi-konstantní vůči šířce sčítačky, ovšem za cenu velkého nárůstu hradel (pro každý full-adder musíme přidat několik širokých AND a jeden široký OR). Velikost prediktoru roste s tím, jak daleko dopředu predikci provádíme. Má tedy smysl udělat určitý trade-off, a predikci někde uříznout. Např. postavit 4b adder s predikcí (velmi rychlý), a ten 4x zřetězit na 16b adder.

Více informací na wikipedii: Carry lookahead adder

Ovšem i po zřetězení 4x 4bit-CLA za sebe není potřeba čekat na ripple-carry propagaci zkrz tyto CLA. Lze použít stejný princip jako předtím, a každý ze čtyř COUT předpovědět ze vstupů ( $P$ a $G$ každého CLA lze vypočítat z $P$ a $G$ full-adderů uvnitř). Jednotce, která toto zaopatřuje se říká Lookahead carry unit (LCU), a je to dobře studovaný obvod.

Více informací na wikipedii: Lookahead carry unit

Varianty

4bit-CLA, 4x zřetězeno - 1b
8bit-CLA, 2x zřetězeno - 2b (relativně velký obvod)
4bit-CLA + LCU - 2b
jiná varianta - dle domluvy

Řešení

Modifikujte svojí existující sčítačku, nevkládejte do ALU další. V OPCODES.txt indikujte místo add operaci cla.

Do full-adderu přidejte výstupy $P$ , $G$ . Pro přehlednost umístěte prediktor do samostatného modulu, který bude brát na vstupu všechny $P_{i}$ , $G_{i}$ , a CIN a na výstupu n-bitový COUT (nebo n-krát $CO U T_{i}$ ).

Pozor

V prediktoru se nesmí vyskytovat řetězec z CIN na nejvyšší COUT, to by mělo stejnou rychlost jako RCA. Je potřeba výraz pro predikci každého bitu plně vyexpandovat a vyjádřit jako součet násobků / sum of products (SOP) / disjunktivní normální formu (DNF), a zapojit pomocí vícevstupových hradel.

Logický posun A doprava/doleva o B míst (Barrel shifter) (~2b)

Pro implementaci posunu o libovolný počet míst se nabízí několik variant, nejefektivnější z hlediska využití tranzistorů je tzv. cross-bar shifter. Nicméně používá třetí stav (controlled buffery nebo na úrovni tranzistorů transmission gates), a proto není vhodný pro implementaci na FPGA, které třetí stav nepodporují.

Princip spočívá v rozložení velikosti posunu na součet mocnin dvou (to je jeho binární reprezentace, tu už máme!), a postupného provedení posunu o každou složku součtu zvlášť. Např. posun o 10 provedeme posunem o 8 a o 2 (posun o 4 a o 1 neprovedeme). Provedení/neprovedení posunu se dá přepínat multiplexorem.

Přehledný diagram implementace tohoto postupu se poměrně špatně hledá, proto ho uvádím zde:

Barrel Shifter pomocí $lo g_{2} n$ multiplexorů (zdroj)

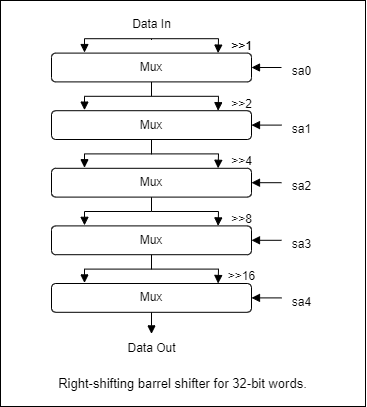
Pro plný počet bodů je potřeba implementovat shift doleva i doprava, v jedné ze dvou variant:

Varianty

bsh - posun doleva pokud $CIN = 1$ , jinak posun doprava
bshl+bshr - posun každým směrem jako zvlášť operace ALU (vhodné pokud vám zbývá dost volných hodnot selectoru)

Info

Není potřeba řešit CIN a COUT jako u shl/shr.

Posun u 16bit hodnot dává smysl provádět o 0-15 míst, posun o více má za výsledek vždy 0. Vaše operace nemusí správně řešit větší hodnoty posunu než 15, stačí tedy brát v potaz pouze spodní 4 bity B.

Konverze z binárky na BCD (~2b)

Implementujte v ALU modul, který převede hodnoty 0-9999 na vstupu A na čtyřmístnou reprezentaci čísla v Binary Coded Decimal (BCD). Tato reprezentace je vhodná pro e.g. zobrazování hodnot v desítkové soustavě na 7-segmentovém displeji. Toto zobrazování budete mít následně jednodušší implementovat jako output v CPU, címž si zajistíte nějaké body za CPU IO.

Tedy $OUTP_{[3:0]}$ bude obsahovat jednotky, $OUTP_{[7:4]}$ desítky, $OUTP_{[11:8]}$ stovky a $OUTP_{[15:12]}$ tisíce hodnoty na vstupu $A$ interpretované v desítkové soustavě. Čísla na vstupu větší než 9999 nemusíte řešit. Takové čísla se vejdou do 14 bitů, takže stačí pracovat s těmito spodními bity vstupu.

Algoritmus, kterým se tento převod dá efektivně (bez dělení a modula!) provést, se jmenuje Double-Dabble. Dá se implementovat jak v SW (opakovanou aplikací porovnání a přičtení), tak v HW (zařazením za sebe tolik modulů provádějících porovnání+přičtení tak, aby se každému bitu stalo to samé, co v SW rutině). Příklad implementace v HW (pro větší hodnoty než máte zadáno) je na konci článku o Double-Dabble.

Efektivní zapojení

"Double" v algoritmu je pouze logický posun doleva, ten lze realizovat jednoduše úpravou zapojení vodičů do další fáze (je zdarma).

V jádrové operaci algoritmu "porovnání a podmíněné přičtení" se porovnává s konstantou (>4), a přičítá konstanta (+3). Obvody pro provedení těchto operací jdou oproti obecnému porovnání a sčítání dramaticky zjednodušit:

Buď, jako jsme delali při úpravě výrazů v Booleově algebře (konstantní jedničky a nuly ve výrazu vždy lze nějak zjednodušit) - rozkreslit si 4b komparátor a 4b sčítačku s těmito konstantami na vstupu a zjednodušovat pomocí booleovy algebry (zapisovat hodnoty konstantních vodičů a škrtat nepotřebná hradla). Samotné rozhodnutí lze vyřešit malým multiplexorem.
Přistupovat k modulu jako funkci o 4 vstupech a 4 výstupech, jejíž pravdivostní tabulku známe, testy sestavit vzorce pro každý z výstupů lze jednoduše pomocí Karnaughovy mapy.

Pouze řešení s efektivním komparátorem a zvětšovačkou bude hodnoceno plným počtem bodů.

APS Skripta