Binární odčítačka
Odčítání jako sčítání
Sice lze postavit dedikovaný obvod, který umí odečíst dvě čísla, podobným postupem jako u sčítačky, akorát podle odčítání pod sebou.
Nicméně o odčítání se dá uvažovat jako o přičítání záporných čísel, v matematice je to běžná věc.
Pokud bychom tedy byli schopní vytvořit nějaký jednoduchý obvod, který z umí vytvořit nějakou hodnotu , kterou můžeme přičíst k , abychom dostali , můžeme pro odčítání použít naši existující sčítačku.
Záporná čísla
Číslu z předchozího příkladu budeme říkat zaporné číslo. Samozřejmě se pořád pohybujeme v digitální logice, toto číslo bude v počítači muset být reprezentované nějakou sekvencí a . Způsobů, jak to udělat, je hned několik (stejně jako u kladných čísel jsme měli binární kód, Grayův kód a BCD), a každá reprezentace bude mít své výhody a nevýhody.
V každém případě předpokládáme, že šířka našeho čísla v bitech je konstantní, protože naše sčítačka/ALU/CPU bude umět pracovat vždy s přesne -bitovými čísly.
Přímý kód (sign-magnitude)
Asi nejjendodušší, co vás napadne, je do jednoho z bitů (zpravidla největšího) "prostě" uložit znaménko zakódvané jako nebo , a zbytek bitů interpretovat jako normální číslo.

Tato reprezentace má několik nevýhod, zejména:
- Pro sčítání těchto čísel je potřeba speciální sčítačka, zčásti protože:
- Máme dvě různé nuly, a , tedy i porovnávání čísel je komplikovanější
- Odčítání nelze realizovat jednoduše jako přičtení záporného čísla
Aditivní kód (offset binary)
Další přirozený způsob spočívá v posunutí nuly "doprostřed" reprezentovatelného rozsahu - směrem nahoru budou kladná, směrem dolů záporná. Tedy v případě 8-bit čísel, kde máme 256 různých čísel, můžeme dát nulu na číslo , takže bude a bude .
Jedná se v podstatě o přímý kód, ale s opačným významem bitu znaménka, má stejné nevýhody.
Jedničkový doplňěk (one's complement)
Další dva možné způsoby reprezentace spočívají v hledání opačných prvků ke kladným číslům pomocí nějakého vzorce. Nejjednodušší takový vzorec je najít záporné číslo pomocí bitwise negace.
Tedy bude a . Protože je , bude , a podobně.
Tento kód má zase podobné nevýhody.
Dvojkový doplněk (two's complement)
Pojďme zkusit vymyslet takový kód, který bude mít vhodnou reprezentaci záporných čísel, abychom odstranili nevýhody ostatních kódů. Tedy chceme mít pouze jednu nulu, chceme aby kladné čísla měla stejnou reprezentaci jako bez znaménka, a chceme, aby šlo odčítat přičtením záporného čísla:
Když pracujeme s n-bitovými čísly, tak vlastně pracujeme s groupu , protože hodnoty a větší neumíme reprezentovat a horní bity zahazujeme (carry).
Např. sčítáme 8-bit čísla, pohybujeme se v :
Chceme označit některá čísla z této grupy jako záporná tak, aby platily následující pravidla:
- Pro každé kladné (které reprezentujeme jako číslo bez znaménka) musí existovat takové , aby platitlo .
- To je ekvivalentní tvrzení
Hledané je tedy aditivní inverzí v . Tu umíme aritmeticky najít:
Pokud toto pravidlo budeme aplikovat na nezáporná čísla počínaje nulou (která je korektně sama svojí vlastní inverzí), začneme záporným číslům přiřazovat reprezentace. Přestaneme, jakmile nám dojdou volná čísla (číslo, které jsme označili jako záporné už nemůžeme zároveň považovat za kladné). Pro n=3 skončíme s následujícím přiřazením:
| Binární řetězec | Bez znaménka | Dvojkový doplněk? |
|---|---|---|
000 | 0 | 0 |
001 | 1 | 1 |
010 | 2 | 2 |
011 | 3 | 3 |
100 | 4 | 4 nebo -4 ? |
101 | 5 | -3 |
110 | 6 | -2 |
111 | 7 | -1 |
Tento kód ja zajímavý tím, že není nemá symetrický rozsah, tedy stejný počet kladných a záporných čísel. To vyplývá automaticky z požadavku mít pouze jednu nulu, přičemž čísel je pořád sudý počet. "Lichý" binární řetězec můžeme přiřadit buď číslu nebo , výsledný kód bude fungovat stejně, protože nad platí, že . Vlastně tedy (stejně jako pro nulu), platí, že .
Tvoří prvky dvojkového doplňku a sčítání stále grupu?
Tvoří prvky dvojkového doplňku a sčítání stále grupu?
Ano, pouze jsme prvkům dali jiné názvy. Operátor nad nimi se chová pořád stejně jako v původním . Mezi sčítáním čísel bez znaménka a ve dvojkovém doplňku není na binární úrovní žádný rozdíl. To znamená, že pro sčítání čísel ve dvojkovém doplňku můžeme používat stejnou sčítačku, jako pro nezáporná čísla!
Musíme se tedy při tvorbě kódu rozhodnout, jestli chceme více záporných a více kladných čísel, aby šly čísla jednoznačně interpretovat. Pokud se rozhodneme "lichému" řetezci přiřadit zápornou hodnotu, získáme pro nás kód navíc jednu velmi hezkou vlastnost:
| Binární řetězec | Bez znaménka | Dvojkový doplněk |
|---|---|---|
0 00 | 0 | 0 |
0 01 | 1 | 1 |
0 10 | 2 | 2 |
0 11 | 3 | 3 |
1 00 | 4 | -4 |
1 01 | 5 | -3 |
1 10 | 6 | -2 |
1 11 | 7 | -1 |
Nejmohutnější (most significant) bit binárního řetězce ve dvojkovém doplňku přímo odpovídá znaménku čísla!
Tomuto kódu, jak jsem jej teď sestavili, se říká dvojkový doplněk nebo doplňkový kód, a používá jej drtivá většina architektur a jazyků pro reprezentaci záporných čísel.
Rozdělili jsme tak grupu na dvě stejně velké poloviny: zápornou a nezápornou:
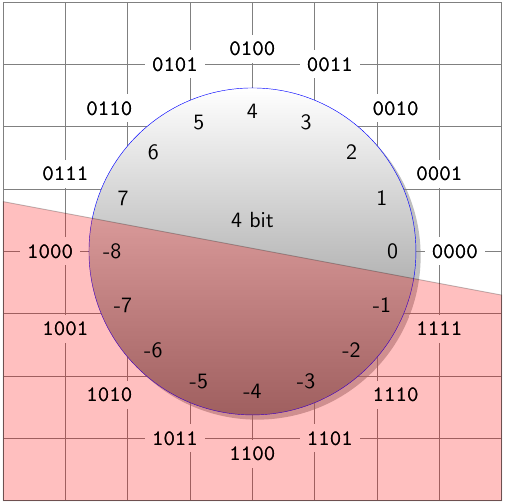
Konkrétní příklad
Co se vlastně na pozadí děje, když odečteme pomocí této techniky nějaké číslo?

Pracujeme s 4-bitovými čísly, tedy (bez znaménka) v . Se znaménkem pracujeme v doplňkovém kódu ona obrázku.
Chceme spočítat . Nalezneme opačnou hodnotu pro číslo :
Výsledek můžeme oveřit na obrázku. Takže z našeho příkladu se stane:
Získali jsme správný výsledek. Pozorujeme, že odčítání vlastně funguje pomocí přičtení "velkého" čísla, což způsobí přetečení o "tak akorát" velké číslo, abychom dostali správný výsledek. Znamená to, že carry-out už nám bohužel nemůže nic říct o tom, zda je výsledek validní.
Lze spočítat absolutní hodnotu z libovolného čísla ve dvojkovém doplňku?
Lze spočítat absolutní hodnotu z libovolného čísla ve dvojkovém doplňku?
Ne bez zvětšení počtu bitů. Pro 3-bitové číslo :
ale lze reprezentovat pouze ve 4- a více-bitových číslech.
Je to opravdová situace, která může nastat ve strojových číslech se znaménkem:
fn main() { let min = std::i8::MIN + 1; // -128 + 1 = -127 println!(" min: {}", min); println!("|min|: {}", min.abs()); }
fn main() { let min = std::i8::MIN; // -128 println!(" min: {}", min); println!("|min|: {}", min.abs()); }
Validita výsledku, přetečení (carry) a přeplňení (overflow)
U sčítání jsme měli výstup carry, který nám indikoval, že výsledek se nevejde do šířky výstupu sčítačky. Tomu jevu se říkalo přetečení.
U záporných čísel se to trochu komplikuje - jak jsme si ukázali na příkladu, zde nám carry může a nemusí nastat ikdyž je výsledek validní. Tedy "přetečení" neboli carry nám nepomůže.
Potřebujeme vymslet jiný indikátor toho, jestli operace ve dvojkovém doplňku byla validní. Pokud tomu tak nebude, budeme tomu říkat přeplňení (overflow).
Přeplnění nastane, pokud hodnota "vyjede" z reprezentovatelného rozsahu. U čísel se znaménkem to může být směrem nahoru (mělo vyjít číslo vyšší, než to nejvyšší reprezentovatelné) nebo směrem dolů (menší než nejmenší reprezentovatelné).

Danou operací sčítaní nebo odčítání se můžeme na kruhu posunou pouze o půlkruh. Tedy, pokud se budeme pohybovat směrem k nule, musíme garantovaně skončit v druhé půlce kruhu, a naše odpověď bude validní. Např. pokud jsme v záporných číslech a přičítáme, skončíme nejdál o půlkruh dál v kladných číslech, na správném výsledku.
Pokud tedy sčítáme kladné a záporné číslo, nemůže přeplnění nastat.
Problém nastává, pokud máme záporné číslo a chceme dále odečítat, nebo máme kladné číslo a chceme dále přičítat. Tedy, přeloženo pouze na součty, máme záporné číslo a chceme přičíst záporné číslo, nebo máme kladné číslo, a chceme přičíst kladné číslo. Tam by se mohlo stát, že se přehoupneme přes hranici MIN-MAX, a číslo náhle změní polaritu.
Tedy, pokud sčítáme kladné a kladné číslo, musí být výsledek kladný, aby byl validní.
Podobně, pokud sčítáme záporné a záporné číslo, musí být výsledek záporný.
Jak víme, znaménko je u čísel se znaménkem vždy Most Significant Bit hodnoty, můžeme tedy sestavit pravdivostní tabulku pro vyhodnocení overflow:
| A | B | A+B | Overflow? |
|---|---|---|---|
| + | - | X | 0 |
| - | + | X | 0 |
| + | + | + | 0 |
| + | + | - | 1 |
| - | - | - | 0 |
| - | - | + | 1 |
Tento signál si pojmenujeme overflow a vyvedeme taky z ALU, podobně jako cout, bude užitečný procesoru v rozhodování o validitě operací se znaménkem.
Efektivní hledání opačného čísla ve dvojkovém doplňku
Našli jsme tedy pěkný kód, který nás nechá pro odčítání recyklovat naši existující sčítačku. Ale, abychom doopravdy mohli odčítat, musíme být schopni rychle nalézt k danému číslu jeho opačné číslo.
Vzorec pro opačné číslo v doplňkovém kódu je následující:
...ovšem pro výpočet tohoto vzorce musíme umět odčítat. Je potřeba se tohoto odčítání nějak "zbavit" a nahradit ho jinou operací, kterou spočítat umíme.
S trochou algebry získáme:
v tomto výrazu je konstanta, která má podobu binárního řetězce samých jedniček o délce . Odečtením libovolného čísla od takové hodnoty nikdy nenastane žádný přenos a odečítaná hodnota se touto operací jednoduše zneguje (vyzkoušejte odečtením pod sebou na papíře), tedy . Dosazením do původního vzorce dostáváme
což je vzorec pro efektivní výpočet opačného čísla ve dvojkovém doplňku v hardwaru. Pozor, pokud je dvojkový doplňěk n-bitový, musí i negace být n-bitová!
Tedy, pokud chceme odečíst dvě čísla A, B, stačí provést:
Pokud chceme odčítat, přivedeme tedy na vstup B naší odčítačky invertovanou hodnotu. Na první pohled se zdá, že budeme muset provést dva součty, nicméně lze na naší sčítačce zajistit pomocí vstupu cin, který při odčítání zafixujeme na kostantní 1.
Z poloviční odčítačky na úplnou
Tím, že jsme takhle použili cin, jsme znemožnili řetězení více menších rozdílů pro provedení většího, jako to šlo u sčítání. Hovoříme tedy o poloviční odčítačce (half-subber). Jak tedy tuto funkcionalitu obnovit, a získat plnou odčítačku (full-subber)?
U odčítání se řetězení provádí pomocí tzv. výpůjčky (borrow). Pokud je borrow-in , odečteme ještě o jedničku více (podobné ale opačné chování jako carry). Na výstupu odčítačky je naopak borrow-out, který signalizuje přetečení do záporných hodnot, tedy v dalším řádu se má odečíst jednička navíc (borrow-in).
Pokud do našich výpočtů zahrneme borrow-in ():
lze podobně jako předtím vyjádřit jako . Máme tedy:
Tuto operaci opět provedeme na naší sčítačce, jako cin při odčítání přivedeme . borrow-in je tedy pouze invertované carry-in.
Kvůli neuvedeným skutečnostem (doplňkový pseudokód) platí to samé pro borrow_out:
Tedy abychom dostali borrow_out pro odčítání, stačí znegovat carry_out z výše uvedeného součtu.
Obecně tedy platí, že carry u sčítání a borrow u odčítání jsou přesné opaky. Tedy pokud převádíme odčítání na sčítání, je potřeba převést borrow-in na carry-in, provést součet, a poté převést výsledný carry-out na borrow-out.
V ALU bude typicky pouze jeden carry-in a jeden carry-out výstup. Tyto IO mají pak dvojí smysl, během sčítání zastávají funkci carry, a během odčítání borrow.
Sčítačka-Odčítačka
ALU musí samozřejmě umět nějěnom odčítat, ale i sčítat. Nestačí tedy zkonvertovat sčítačku na odčítačku. Taky není dobré řešení mít dvě sčítačky, jednu na sčítání a odčítání, když ALU děla v jeden čas vždy pouze jednu z obou operací, to je v ALU penalizováno.
Je tedy potřeba postavit modul sčítačka-odčítačka, který umí obojí, a má speciální vstup (může se jmenovat např. sub jako subtract), kterým lze zapnout režim odčítání.
- V režimu sčítání bude počítat .
- V režimu odčítání bude počítat (varianta
half_sub)- Tedy se nebere v potaz, výstup je zapojen stejně jako u součtu.
- Alternativně v režimu odčítání bude počítat (varianta
full_sub)- mají korektní borrow chování ve dvojkovém doplňku, viz "Jak zřetězím dve odčítání"
- je jeden vstup pojmenovaný
CINneboCIN_BIN, který přepíná své chování podle toho, zda se zrovna odčítá. - stejně.
Implementace
Pro implementaci této komponenty je samozřejmě potřeba mít jako modul hotovou sčítačku. Poté stačí pomocí vhodných multiplexorů podle vstupu sub vybírat, jaké hodnoty vlastně na vstupy sčítačky chceme přivést, případně jaké hodnoty (třeba vypočtené z výstupů sčítačky) chceme vyvést na výstupy modulu.