Karnaughova mapa
Karnaughova mapa je prostředek pro minimalizaci logických obvodů. Pro pochopení Karnaughovy mapy musíme první pochopit Grayův kód.
Grayův kód
Grayův kód je binární číselná soustava, ve které se každé dvě po sobě jdoucí hodnoty liší v jedné bitové pozici.
Příkladná tabulka pro 3 bity (tučně zvýrazněný změněný bit):
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 0 | 0 |
Karnaughova mapa - příklad 1
Máme pravdivostní tabulku se vstupy a výstupem :
| A | B | C | D | Q | index bitu |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 2 |
| 0 | 0 | 1 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 0 | 5 |
| 0 | 1 | 1 | 0 | 0 | 6 |
| 0 | 1 | 1 | 1 | 0 | 7 |
| 1 | 0 | 0 | 0 | 1 | 8 |
| 1 | 0 | 0 | 1 | 1 | 9 |
| 1 | 0 | 1 | 0 | 1 | 10 |
| 1 | 0 | 1 | 1 | 1 | 11 |
| 1 | 1 | 0 | 0 | 1 | 12 |
| 1 | 1 | 0 | 1 | 1 | 13 |
| 1 | 1 | 1 | 0 | 0 | 14 |
| 1 | 1 | 1 | 1 | 0 | 15 |
- Vytvoříme tabulku pomocí indexů v pravdivostní tabulce (odvíjí se od Grayova kódu). Neboli doplníme do obrázku
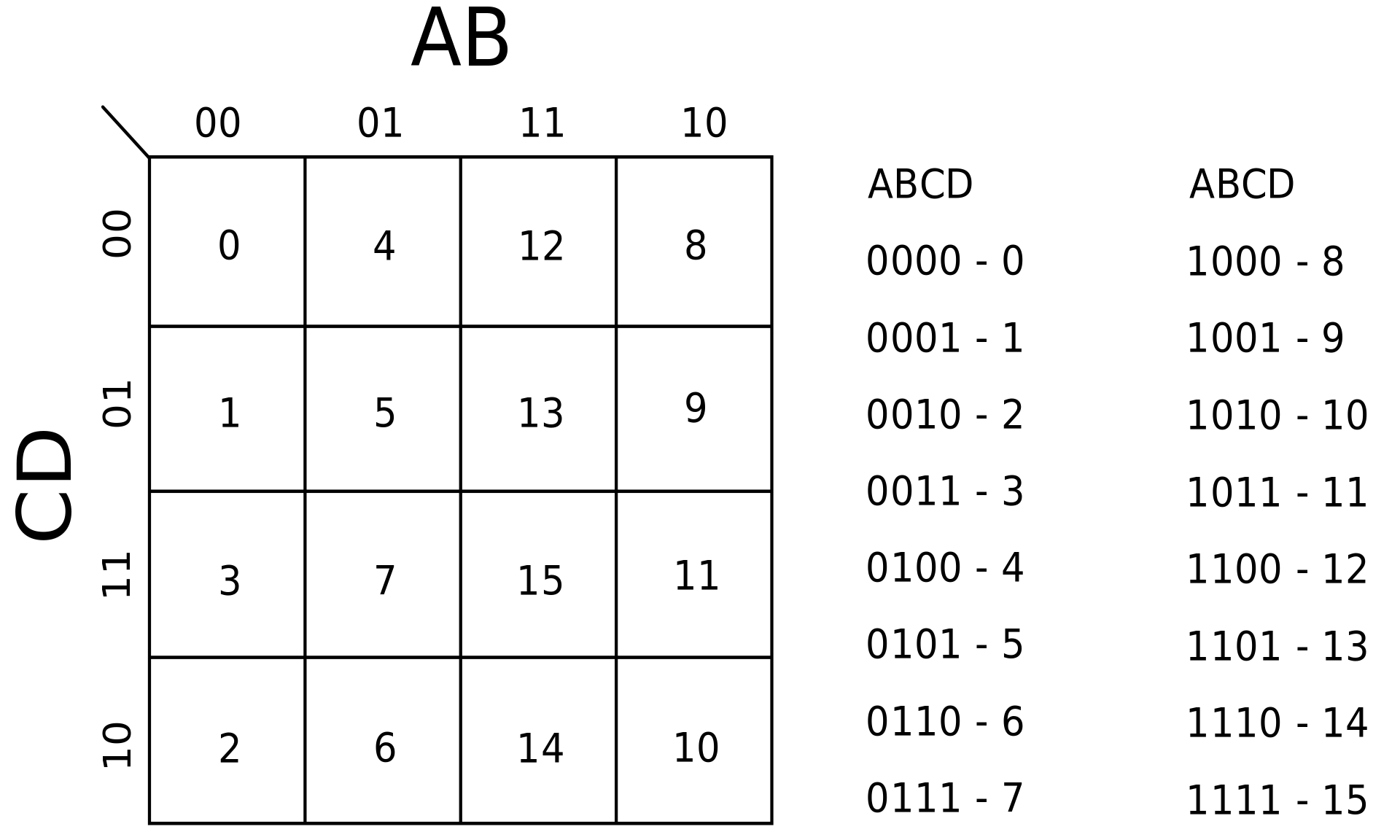
Vznikne nám následující tabulka
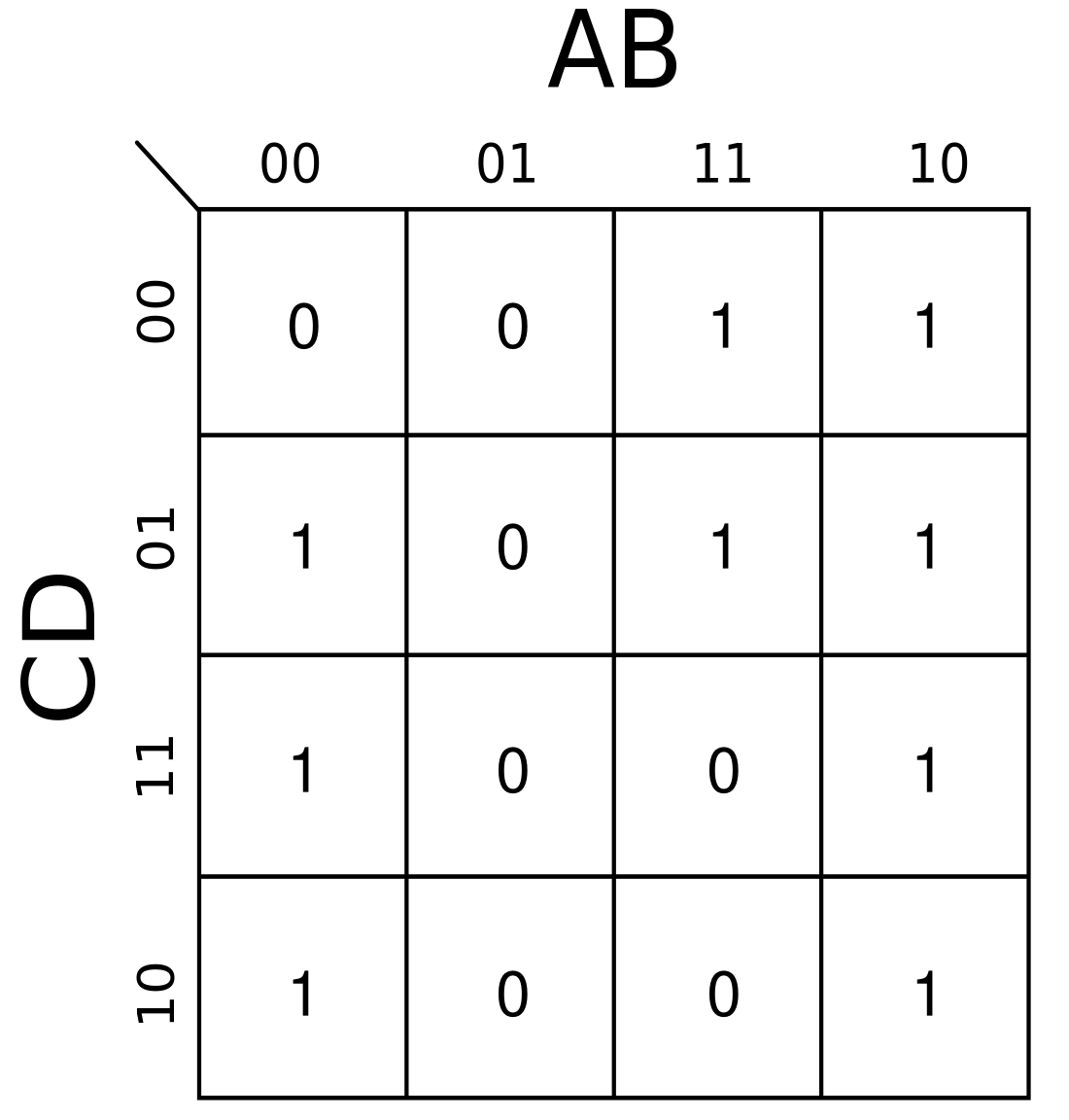
- Zakroužkujeme sousedy
Musíme zakroužkovat všechny , kroužkujeme buď samostatnou (v tomto případě je výsledek stejný jako při stavění pomocí mintermů přímo z pravdivostní tabulky, tady K-mapa nemá žádný přínos) nebo obdélníky s obsahem rovným některé mocnině , z čehož přímo výplývá (jako nutná podmínka), že obě dělky stran obdélníků musí být mocniny dvou.
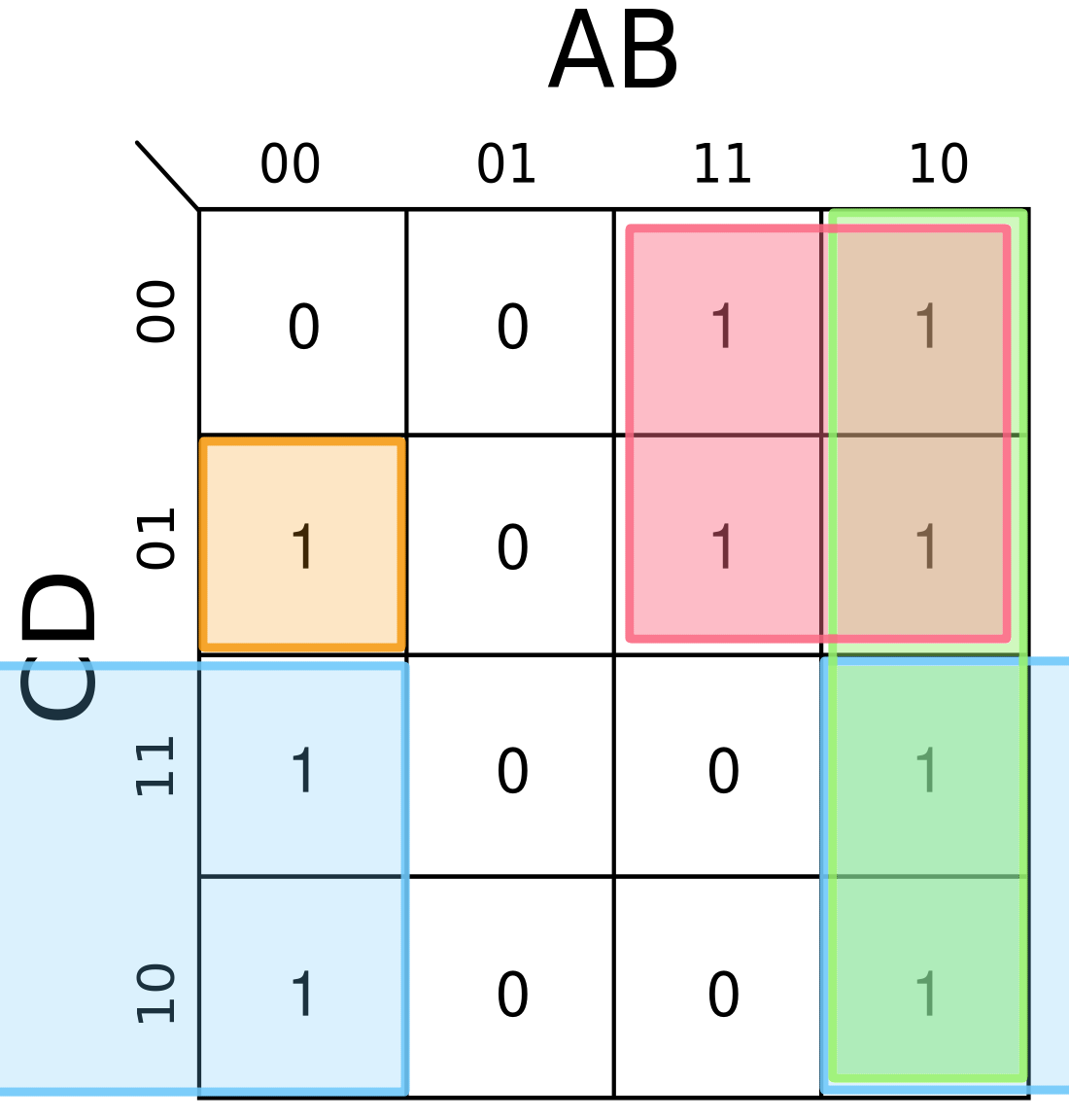
- Vytvoříme výrazy
- Růžová -
- Zelená -
- Modrá -
- Oranžová -
- Sečteme výrazy
- Upravíme výraz
Karnaughova mapa - příklad 2
Máme pravdivostní tabulku se vstupy a výstupem :
| A | B | C | Q |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
- Vytvoříme si Karnaughovu mapu (tam kde jsou písmena, tak je hodnota nastavená na 1)
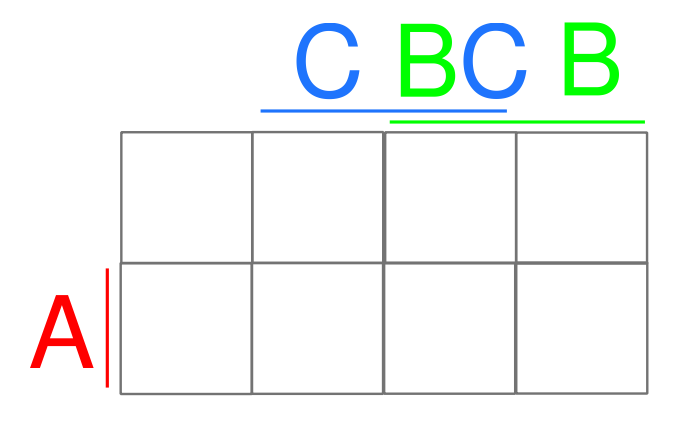
- Doplníme do tabulky

- Zakroužkujeme největší obdelníky a vyjádříme je
POZOR: oranžový 1x1 obdélník není optimální (maximální), lepší by byl jako 2x2 čtverec přecházející přes hranu. Je to takhle zvolen abychom ukázali, že K-Mapa dál funguje, jenom není výsledek optimální - 1x1 čtverec je potřeba vyjádřit jako 4-term, místo 2-termu pokud bychom udělali 2x2.

Vidíme, že je blok nezávislý na tom, jestli je nebo , takže zahrneme jen proměnou a
- musí být
- musí být
Součin jsme použili, protože je totožné logickému a zároveň platí (v programovacím jazyku C -->&&)
Jelikož se jedná o torus (viz. gif), můžeme označit i hodnoty, které se nacházejí "vedle sebe" (na začátku a na konci)


Vidíme, že je výraz nezávislý na proměnné (může být nebo )
- musí být
- musí být
- Sjednotíme výrazy
Výsledné výrazy sečteme
- Výsledný výraz si můžeme postavit v logisimu viz. obrázek
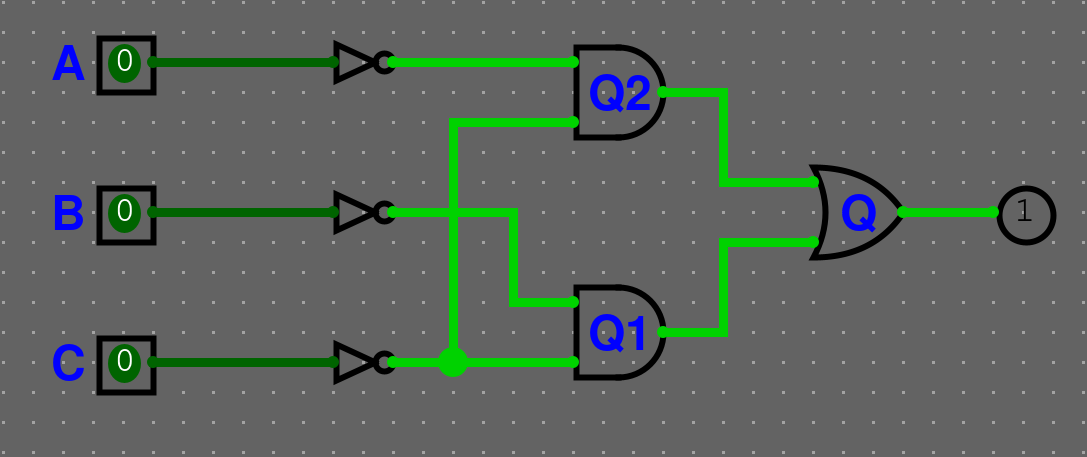
- Zkontrolujeme pravdivostní tabulku.
- Klikneme pravým tlačítkem na circuit v nabídce (základní je main)
- Klikneme na tlačítko Build Circuit
- Potvrdíme tlačítkem OK, popřípadě Yes
- Vybereme v nabídce Table
- Dostaneme tabulku viz. obrázek
