Paměti - Sekvenční obvody
Kombinační obvody
Kombinační obvody lze ekvivalentně zadefinovat několika způsoby:
- Hodnoty výstupů jsou plně definované pouze hodnotami vstupů
- Obvod implementuje matematickou funkci, tj. lze popsat pravdivostní tabulkou
- V obvodu se nevyskytují žádné cykly (nepřímá závislost vstupu hradla na jeho výstupu)
Příklad kombinačního obvodu
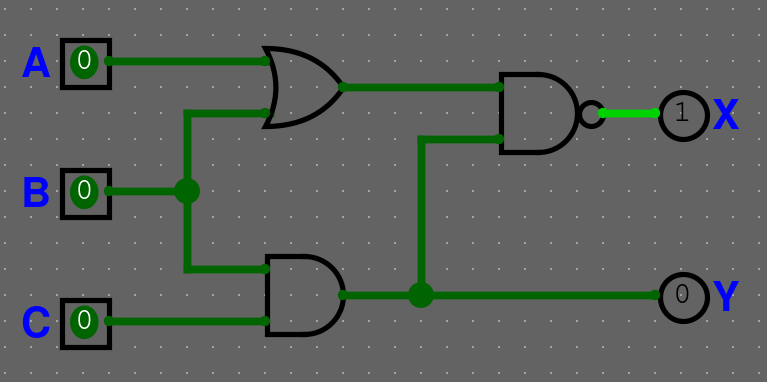
Sekvenční obvody
Sekvenční obvody jsou ty obvody, které nejsou kombinační, tj. vyskytují se v nich nějaké cykly. Tyto cykly způsobují zajímavé chování (paměť), ale jsou obtížnější analyzovat.
Příkladný sekvenční obvod s OR
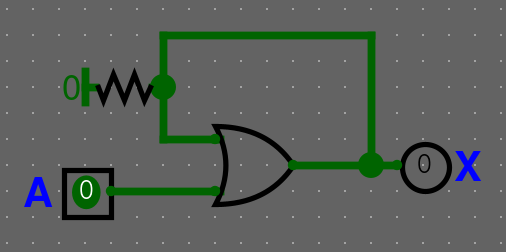
Znázornění v pravdivostní tabulce
Protože X je zároveň výstup a vstup do obvodu, musíme tyto dvě jeho funkce rozdělit:
- - aktuální hodnota vodiče X, tj. vstup
- - příští hodnota vodiče X, tj. výstup.
"Příští" tady znamená, jakmile dané hradlo zpracuje své vstupy a aktualizuje svůj výstup - jeho tzv. propagační delay, který je vždy nenulový, závislý na výrobním procesu (typická hodnota např. 10ns). Tedy je to hodnota X v budoucnosti.
Nyní v pravdivostní tabulce můžeme popsat, jaké bude příští X v závislosti na aktuálním X a vstupu :
| A | X | X' |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Z chování obvodu vidíme, že pokud je , se nezmění (), a pokud , pak na nezáleží a . Můžeme tedy pravdivostní tabulku zjednodušit zavedením neznámé :
| A | X | X' |
|---|---|---|
| 0 | S | S |
| 1 | S | 1 |
V této tabulce může S nabýt libovolných hodnot ( nebo ) a každá varianta reprezentuje jeden řádek. Nicméně z takto zjednodušené tabulky je lépe vidět časové chování obvodu:
Pokud se obvod nachází v nějakém "stavu" , tak při v něm zůstane, ale při přejde do stavu .
Zároveň platí, že abychom mohli znát hodnotu výstupu, musíme znát hodnotu aktuálního stavu , který může být skrytý uvnitř obvodu, nestačí nám pouze vstup - typická vlastnost sekvenčních obvodů.
Popis výrazem a nekonečné vyhodnocování
Obvod můžeme popsat i výrazem:
kde značí příští hodnotu a tu stávající. Pokud nám ale vyjde jiné , než jsme měli , obvod na něj okamžitě zareaguje (je to vstup) a spustí výpočet znovu po dosazení za , tedy potenciálně je nutné popsat obvod takto:
Zde vidíme, že výraz se po opakovaném (klidně i nekonečném) dosazování za nemění. Z toho lze odvodit, že je garantovaně stabilní. Nemusí tomu tak být vždy
Nestabilní obvody
Nejjednodušší nestabilní obvod je následující obvod o nula vstupech:
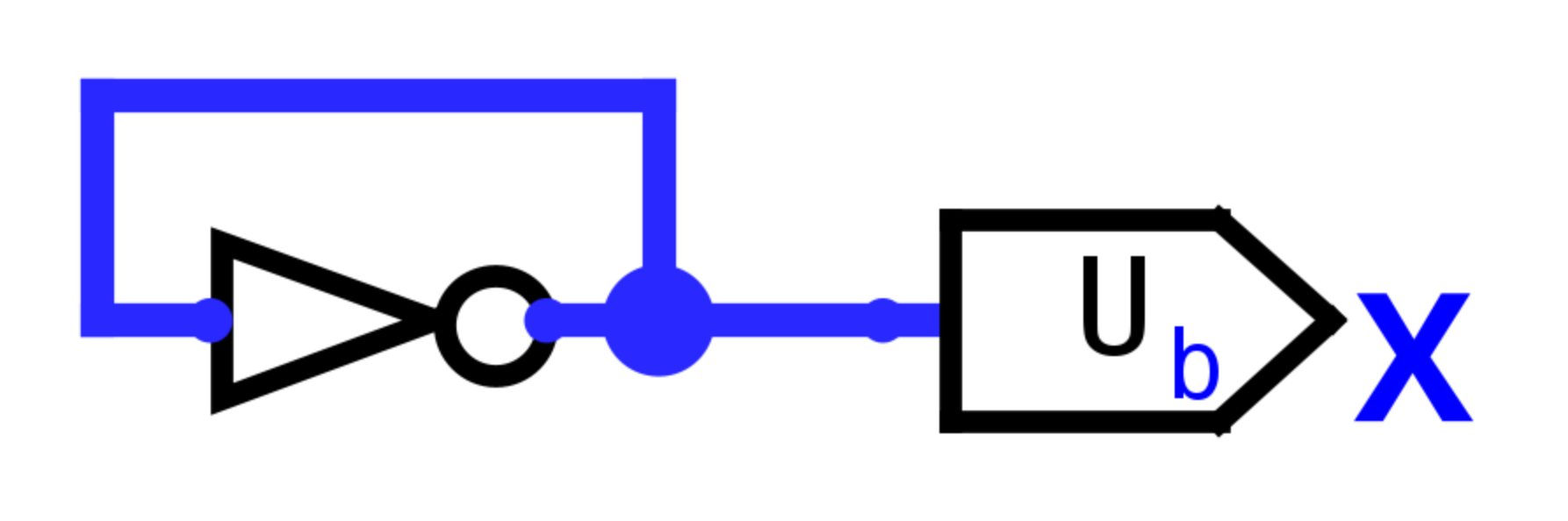
Tento obvod můžeme zase modelovat pomocí výrazu:
Pokud ale budeme opakovaně dosazovat, nedostaneme ten samý výraz. Označme (neznámý) počáteční stav , a stav po dosazeních (neboli po provedeních obvodu). Každý stav se vypočítává z toho předchozího.
Můžeme tedy říct, že protože a obecně , stav obvodu se po každém provedení hradla změní, a tedy není stabilní, nikdy se neustálí na jednu stálou hodnotu, neboli osciluje. Skutečně, potvrdí nám to i simulace Logisimem:
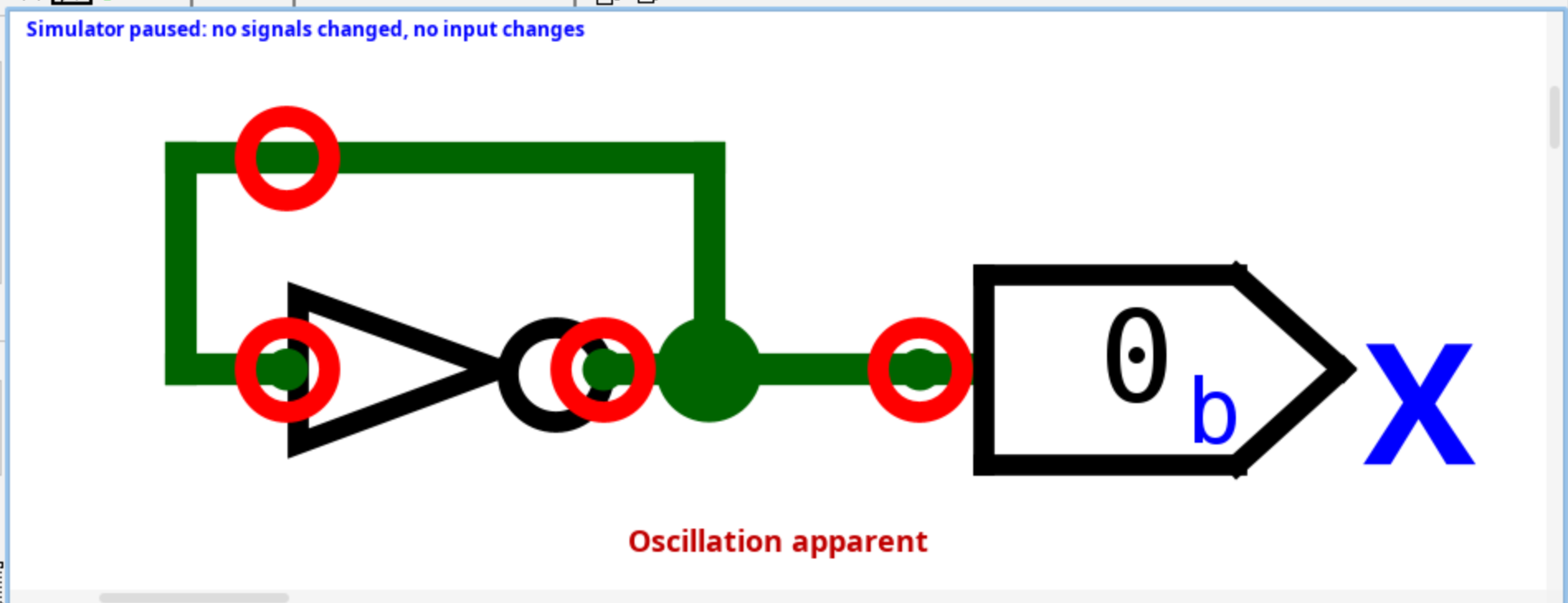
SR Latch
Sekvenční obvody můžete využít pro paměť pomocí hradla OR. Hradlo OR nám vstup zapne a nechá výstup neustále zapnutý, ale nemáme ho zatím jak vyresetovat.

Abychom ho mohli vyresetovat, přidáme další vstup a to R jako reset.
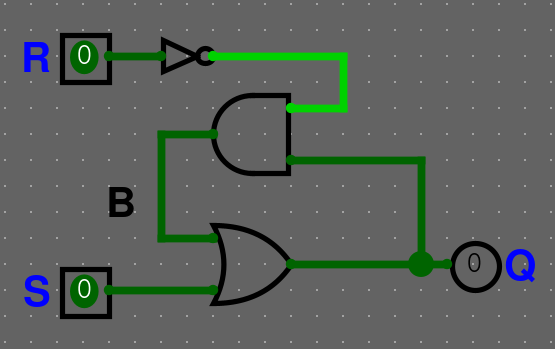
Zapíšeme do výrazu
Zapíšeme chování do pravdivostní tabulky
| R | S | Q | Q' |
|---|---|---|---|
| 0 | 0 | Q | Q |
| 0 | 1 | X | 1 |
| 1 | 0 | X | 0 |
| 1 | 1 | X | 1 |
Vytvořili jsme SR Latch, který se ale dá optimalizovat, tak abychom potřebovali 2 stejné gaty a to NOR viz. gif.
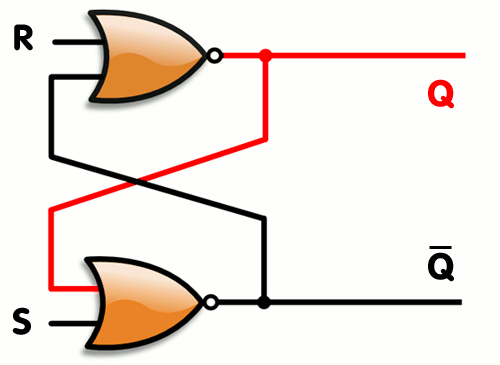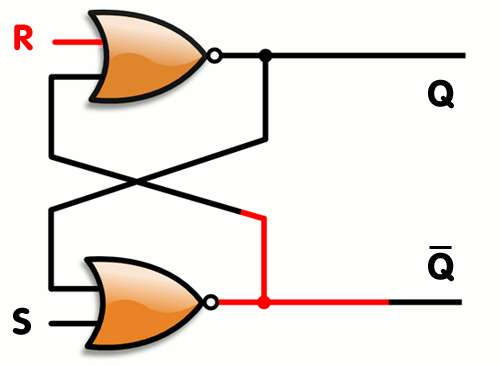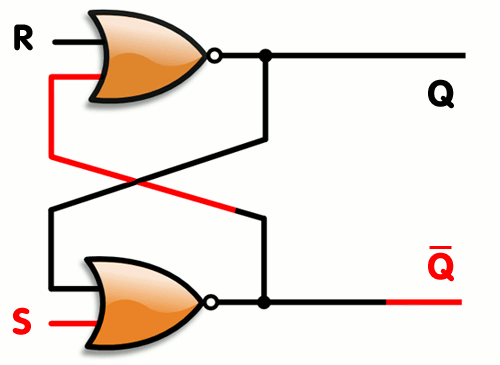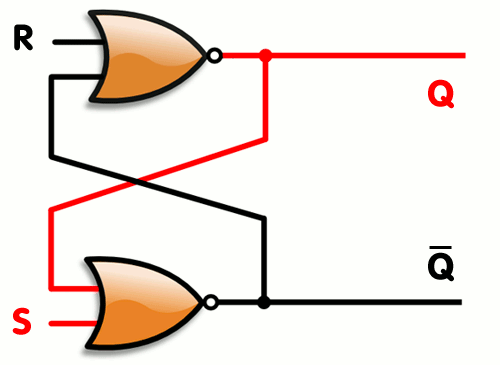
Latch vs Flip Flop
Signály
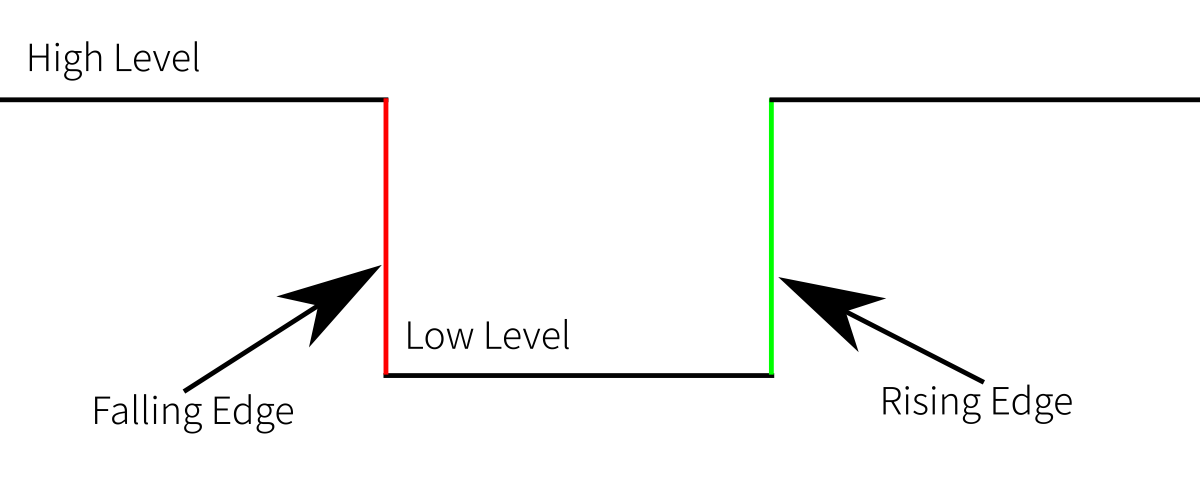
Na následujícím obrázku vidíme 4 definice.
High Level(Active-High) - zde probíhá ukládáníLow Level(Active-Low) - značí se jakoCLKneboENARising/Falling edgehodnota se zpracuje v okamžiku přechoduCLKsignálu z high na low a opačně
Latch
Latch je level-triggered. To znamená, že latch bere vstup, když je zapnutý viz. obrázek
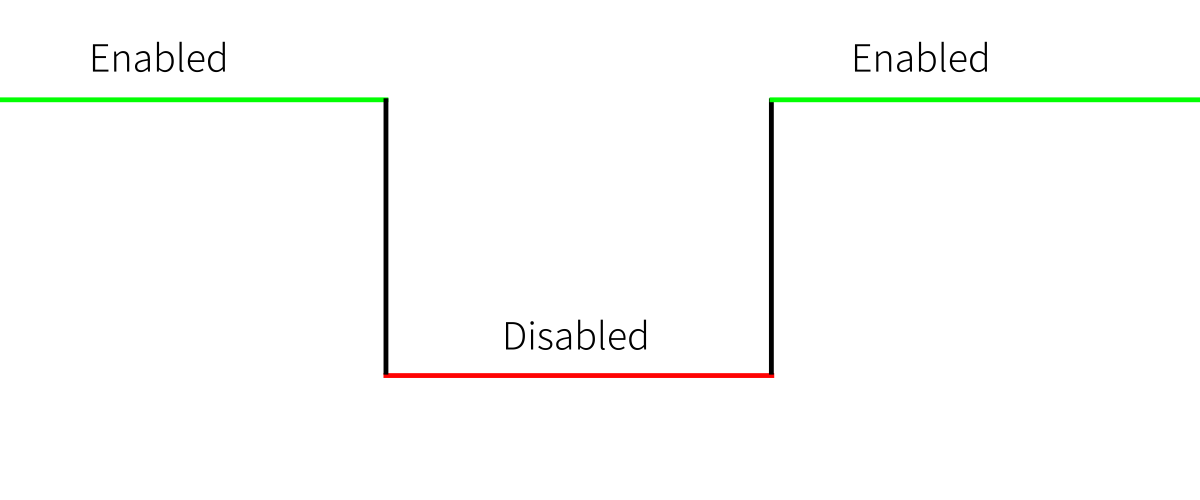
Flip Flop
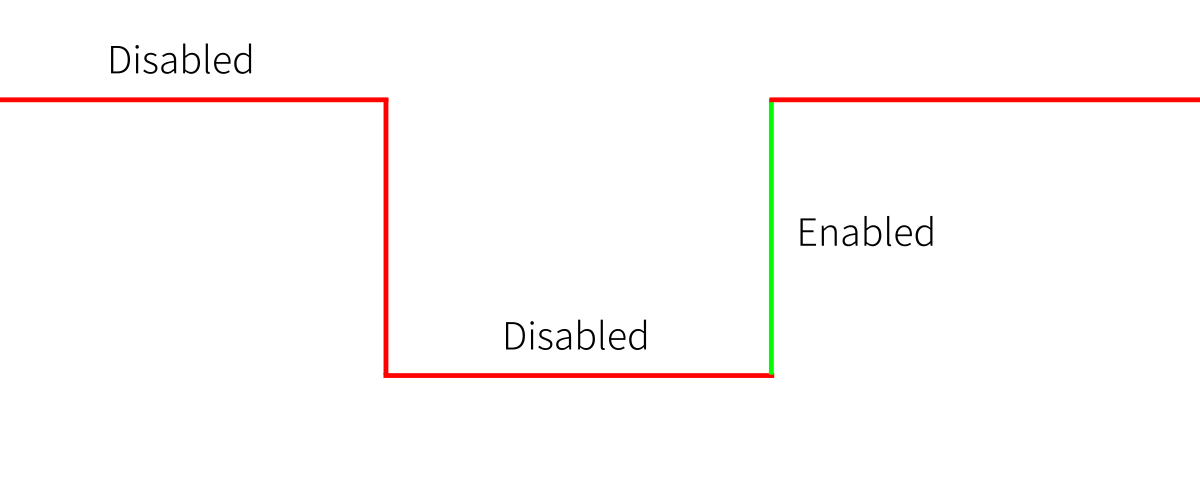
Flip flop je edge-triggered. To znamená, že buď bere vstup na rising edge nebo falling edge. Na následujícím obrázku bere vstup na rising edge.
Oscillation apparent
V rámci sekvenčních obvodů můžete narazit na chybu Oscillation apparent. Znamená to, že jste v nějakém paradoxním cyklu. Vyřešíte to následovně:
- Odstraníme problémový prvek
Reset Simulation(CTRL+R)- Pokud není zapnuté tak -->
Auto-Propagate(CTRL+E)
Bonusové materiály
- Latch vs Flip Flop - https://www.youtube.com/watch?v=LTtuYeSmJ2g
- Latch a Flip Flop na wikipedii
- Anglicky (víc informací) - https://en.wikipedia.org/wiki/Flip-flop_(electronics)
- Česky - https://cs.wikipedia.org/wiki/Bistabiln%C3%AD_klopn%C3%BD_obvod