Hradla a operátory Booleovy algebry
Jistě víte, že počítače pracují pouze s jedničkami a nulami. S pomocí pouze těchto dvou hodnot a operací nad nimi jsou schopné řešit libovolně komplikované problémy. Abychom mohli studovat, jak to je možné, musíme si určitým způsobem tyto základní výpočty nad jedničkami a nulami zformalizovat. Později si ukážeme, jak pomocí těchto jednoduchých operací stavět komplikovanější operace, moduly a finálně procesor.
Booleova algebra
Matematickou abstrakci pro výpočty pouze nad hodnotami 0 a 1 popsal v 19. století George Boole, nazývá se Booleova algebra. Tuto algebru můžeme zjednodušeně chápat jako alternativu ke klasické algebře z hodin matematiky - čísla a operace budou mít odlišný význam, než jsme zvýklí. Ovšem, pokud budou tyto operace chytře zvolené, jako v Booleově algebře, zjistíme, že spousta pravidel z klasické matematiky stále bude fungovat.
Výrazy v Booleově algebře
Podobně jako v matematice, budeme se zde zabývat výrazy. V takovém výrazu najdeme operátory, proměnné a neznámé. Např.
Zde je proměnná, která je definovaná tímto výrazem. jsou neznámé - musíme se k nim chovat jako by mohly mít libovolnou hodnotu. jsou operátory, které bychom uměli provést, pokud bychom znali hodnoty .
Nuly a jedničky
Každý výraz, proměnná nebo neznámá může v Booleově algebře nabýt pouze dvou hodnot:
- neboli
falseneboli nepravda neboli např. 0 voltů - neboli
trueneboli pravda neboli např. 5 voltů
U výpočtů v Booleově algebře se budeme držet hodnot a , nicméně je důležité si uvědomit, že tyto hodnoty mají jistý vztah k výrokové logice, která zkoumá, zda-li je nějaký výrok pravdivý (rečeno v Booleově algebře: výraz se rovná ). Zároveň se v praxi pak jedničky a nuly musí nějakým způsobem reprezentovat, například úrovní napětí na nějakém vodiči.
Operátory Booleovy algebry a hradla
Pozadí k operátorům
"Operátor" je pro naše účely symbol, který značí ve výrazu, že by se měla provést nějaké matematická operace, která bude mít nějaký výsledek. Operátory delíme podle počtu jejich argumentů (chcete-li "vstupů"):
- Unární (jeden vstup). V matematice máme např. unární mínus nebo faktoriál:
a - Binární (dva vstupy). Většina operátorů v matematice - sčítání, násobení, ...:
- Ternární a další. V matematice takových moc není, ale např. v programovaní narazíte na ternary conditional operator (a ? b : c).
Operátory v Booleově algebře
Protože v Booleově algebře mohou hodnoty nabývat pouze a , je velmi jednoduché zadefinovat chování takového operátoru: Stačí vypsat všechny možnosti! Takže například násobení () si můžeme zadefinovat takto:
A to je vše! Žádná jiná varianta nemůže nikdy nastat. Když se nad tím zamyslíme, tak ostatní operátory se od násobení budou lišit pouze pravou stranou rovnic - levá strana pouze vyčítá všechny možné kombinace a .
Další binární operátory si můžeme vymyslet vybráním / pro každou ze 4 variant vstupů. Takže binárních operátorů v Booleově algebře je pouze a násobení je jedním z nich. Celkem si zadefinujeme 6 binárních operátorů a 1 unární, které budeme bežně používat.
Pravdivostní tabulka
Uvidíme, že "vypsat všechny možnosti" je docela užitečná věc, nejenom pro základní operátory. Zavademe si tedy pravdivostní tabulku, ve které systematicky všechny možnosti popíšeme:
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Levá část pravdivostní tabulky je nadepsaná vstupy a vyčítá všechny jejich kombinace v přehledném (vzestupném) pořadí. V pravé straně máme výstup, který můžeme označít buď výrazem nebo proměnnou, například .
Pravdivostní tabulka má různý počet řádků podle počtu kombinací a tedy podle počtu vstupů. Každá kombinace vstupů se musí vyskutnout přesně jednou! Takže pro vstupných proměnných bude mít pravdivostní tabulka řádků.
Hradlo
Ke každému, operátoru, který si ukážeme, si zavedeme hradlo. To je "fyzická krabička", která má Booleovské vstupy a výstupy, a umí "provést" danou operaci. Např. pro operaci násobení si zavademe hradlo AND:
Jde nám zde o tvar tohoto hradla, abychom ho uměli na první pohled rozlišit od ostatních. Stejně jako z operátorů lze stavět výrazy, z hradel budeme stavět obvody. Je důležité pamatovat na formální rozdíl mezi "operátorem" a "hradlem", ikdyž budeme používat "násobení" a "AND" zaměnitelně.
Výroková logika
K operátorům a značení, které si ukážeme, existuje ještě alternativní značení v tzv. výrokové logice, které se používá v matematice pro důkazy. Např. místo bychom napsali . Toto značení v tomto předmětu nepoužíváme, je uvedeno pro úplnost.
Unární operátory
Hradla, které mají jeden vstup jsou následující
- Buffer (repeater)
- NOT
Buffer (repeater)
Buffer je hradlo, u kterého výstup přesně kopíruje vstup. Nezavadíme pro něj symbol operátoru, protože je to zbytečné, trochu jako říkat v matematice místo . Nicméně v praxi se toto hradlo používá zejména pro zesílení signálu.
Symbol
Výraz
Matematická definice
Zápis v C
bool A;
bool Q = A;
Pravdivostní tabulka
| A | Q |
|---|---|
| 0 | 0 |
| 1 | 1 |
NOT
Hradlo NOT použijete, když potřebujete změnit hodnotu na její opak.
Neboli 0 → 1 nebo 1 → 0
Symbol
Definice
Matematická definice
Zápis v C
bool A;
bool Q = !A;
Pravdivostní tabulka
| A | Q |
|---|---|
| 0 | 1 |
| 1 | 0 |
Základní hradla se dvěma vstupy
Základní hradla, které mají dva vstupy jsou následující
- AND
- OR
- XOR
AND
Hradlo AND neboli logické "a" , se využívá když chcete naplnit dvě podmíky.
Pokud platí A a B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo AND rovná násobení
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A && B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR
Hradlo OR neboli logické "nebo" , se využívá když chcete naplnit aspoň jednu podmíku.
Pokud platí A nebo B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo OR rovná součtu
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A || B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR
Hradlo XOR neboli exkluzivní OR , se využívá když chcete naplnit pouze jednu podmíku. Jednoduše řečeno, když se sobě nerovnají.
*Pokud platí právě A nebo právě B, tak pošli na výstup hodnotu 1 ... Pokud se A nerovná B
Symbol
Definice
V Booleově algebře se pro hradlo XOR používá symbol
Zápis v C
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = A ^ B;
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Opaky základních hradel se dvěma vstupy
Opaky základních hradel, existují právě 3
- NAND (opak AND)
- NOR (opak OR)
- XNOR (opak XOR)
NAND
Hradlo NAND má opačný výstup hradla AND
Pokud neplatí A a B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo NAND rovná negaci násobení
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A && B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR
Hradlo NOR má opačný vstup hradla OR
Pokud neplatí A nebo B, tak pošli na výstup hodnotu 1
Symbol
Definice
V Booleově algebře se hradlo NOR rovná negaci součtu
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A || B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR
Hradlo XNOR je opak hradla XOR, jednoduše řečeno se jedná o ekvivalenci
Pokud se A rovná B
Symbol
Definice
V Booleově algebře se hradlo XNOR rovná negaci operaci ((\oplus))
Zápis v C:
bool A = <bool_val>;
bool B = <bool_val>;
bool Q = !(A ^ B);
Pravdivostní tabulka
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Cheat sheet
Cheat sheet pro logické hradla
Vstup A a Vstup B dává výstup <operace>
| A | B | AND | OR | XOR | NAND | NOR | XNOR |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
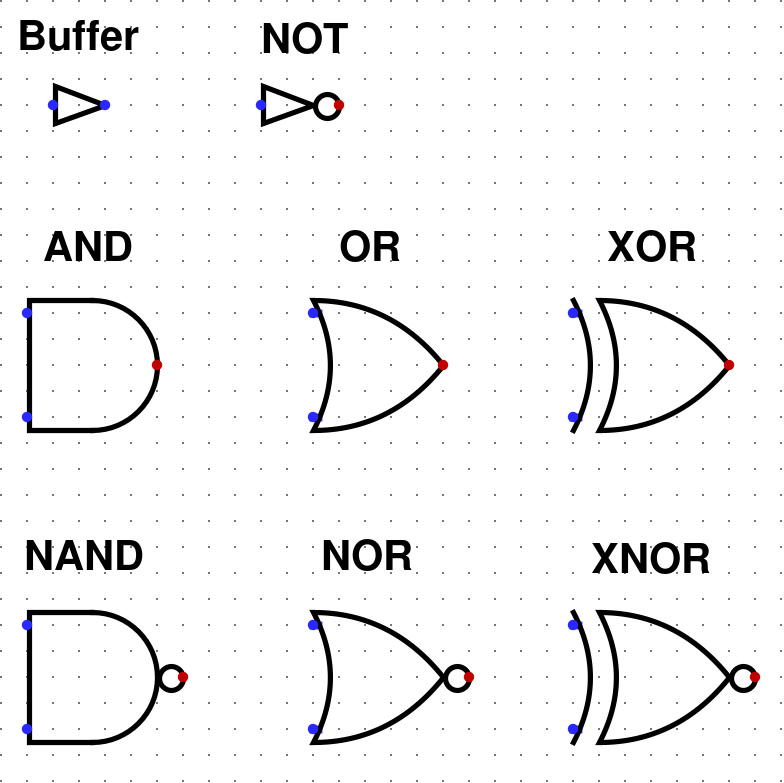
Zobrazení logických hradel v logisimu